Horizontal Martingales in Vector Bundles
by Marc Arnaudon and Anton Thalmaier

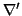Canonical prolongations of manifold-valued martingales to vector bundles over a manifold are considered. Such prolongations require a lift of the connection from the manifold to the corresponding bundle. Given a continuous semimartingale X in M, if $\nabla$ is a connection on M (i.e. a covariant derivative on TM) and $\nabla'$ the lifted connection on E (i.e. 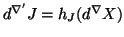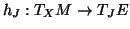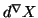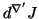a covariant derivative on TE), we consider semimartingales J in E, living above X and linked to X via $d^{\nabla'}J=h_J(d^\nabla X)$where $h_J:T_XM\to T_JE$ is the horizontal lift; $d^\nabla X$ and $d^{\nabla'}J$ denote the Itô differentials with respect to the given connection. Such semimartingales J in E will be called horizontal semimartingales, resp. horizontal martingales in case when X is a $\nabla$-martingale. 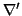There are numerous ways of lifting $\nabla$ to $\nabla'$. We mainly deal with horizontal and complete lifts. Horizontal lifts give rise to the notion of covariant Itô differentials. For covariant Itô differentials a commutation formula with ordinary covariant differentials is established. As an application, covariant variations of stochastic parallel transport and their relation to Yang-Mills connections are investigated. On the other side, within the framework of complete lifts of connections, the martingale property is preserved under taking derivatives (or exterior derivatives) of families of martingales and is inherited to diffusions on the exterior cotangent bundle with the de Rham-Hodge Laplacian as generator. Moreover, in a natural way, derivatives of harmonic maps are harmonic as well.

In: J. Azema, M. Emery, M. Ledoux and M. Yor (Eds.)
Séminaire de Probabilités XXXVI, 419-456,
Lecture Notes in Mathematics 1801,
Springer: Berlin, 2003.

The paper is available here:

Marc Arnaudon <arnaudon@math.univ-poitiers.fr>
Anton Thalmaier <anton.thalmaier@uni.lu>

Back to Homepage