 Back to Homepage
Back to Homepage
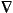 then this topology and the
topology of compact convergence in probability coincide on the set
of continuous
then this topology and the
topology of compact convergence in probability coincide on the set
of continuous 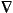 -martingales.
For the topology of manifold-valued semimartingales, we give results
on differentiation with respect to a parameter for second order,
Stratonovich and Itô stochastic differential equations
and identify the equation solved by the derivative processes.
In particular, we prove that both Stratonovich and Itô equations
differentiate like equations involving smooth paths
(for the Itô equation the tangent bundles must be
endowed with the complete lifts of the connections on the manifolds).
-martingales.
For the topology of manifold-valued semimartingales, we give results
on differentiation with respect to a parameter for second order,
Stratonovich and Itô stochastic differential equations
and identify the equation solved by the derivative processes.
In particular, we prove that both Stratonovich and Itô equations
differentiate like equations involving smooth paths
(for the Itô equation the tangent bundles must be
endowed with the complete lifts of the connections on the manifolds).
In: J. Azema, M. Emery, M. Ledoux and M. Yor (Eds.)
Séminaire de Probabilités XXXII, 188-214,
Lecture Notes in Mathematics 1686,
Springer: Berlin, 1998.
The paper is available here: