![[ORIGINAL ARTICLE]](../GRAPHICS/original_article.gif)
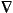-martingales
on manifolds are investigated: their infinitesimal variation provides a notion
of stochastic Jacobi fields.
Such objects are known to be martingales taking values in the tangent
bundle when the latter is equipped with the complete lift of the
connection .
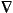We discuss various characterizations of TM-valued martingales and
apply our results to establish formulas in connection with the
stochastic representation of the heat flow for harmonic maps
between Riemannian manifolds. As an application, we give local and global
gradient estimates for harmonic maps of bounded dilatation.
J. Math. Pures Appl. 77 (1998) 283-315
The paper is available here:
Back to Homepage