Gallery
- Lët'z box-counting (project)
-
Voter models and influencers in social networks
(project)
students: Francesca Feyereisen, Oliver Philip Jack, Noah Thielen (report)
Both of these animations illustrate the evolution of the basic 2D voter model, however with different initial setups. In the first GIF, the initial proportions of the two colours are equal, meaning that they both occupy around 50% of the grid at the beginning. In the second GIF, the red colour initially possesses about 75% of the grid, while the blue colour only has around 25%, giving the red colour a clear advantage to dominate the grid eventually.


-
The Collatz conjecture
(project)
students: Antonios Pantelis, Julien Pezzi, Clara Duchossois

-
Illustrating number theory
(project)
students: Jan Huberty, Ibrahim Hukic, Maurice Desquiotz
Two representations for the abelian sand pile model, constructed in the following way: assume that a point in $\mathbb{Z}^2$ contains an integer number (weight) of chips, such that if this number is greater or equal to 4, the position will topple over, equally distributing over the four neighbours of the point. Continuing this way, every position will eventually contain either 0, 1, 2 or 3 chips. The representation is once realized for an initial weight of 500000 chips placed at the origin of $\mathbb{Z}^2$, and for two disjoint weights placed at distinct positions.


-
Eigenvalues of random matrices
(project)
students: Tim Seuré, Max Thill (report)

Marchenko-Pastur: Consider a matrix $Y=XX^{\mathsf{T}}$, where $X$ is a random, real matrix of size $N\times M$ with i.i.d. entries having finite variance. If $M$ and $N$ are large, then the histogram of $Y$'s eigenvalues corresponds roughly to the curve of a function that only depends on $M/N$, $N$ and the variance of $X$'s entries. For the example, we have chosen $N=1500$, $M/N=5$, and $X$'s entries to be normally distributed with mean 50 and variance 1.

Circular law: Consider a random, complex, square matrix $A$ of large size with i.i.d. entries having finite variance. Then $A$'s eigenvalues appear to be roughly uniformly distributed in a complex disc centred at 0, whose radius only depends on $A$'s size and the variance of $A$'s entries. The example shows the eigenvalues of a matrix of size 1500 whose entries are normally distributed with mean 100 and variance 5.

Wigner: Consider a random, real, symmetric matrix $A$ whose entries all have the same finite variance. Under the right assumptions of independence and distribution of $A$'s entries, the histogram of the eigenvalues corresponds roughly to a half-ellipse whose axes only depend on $A$'s size and its entries' variance. The example shows the histogram corresponding to a matrix $A$ of size 1500, whose entries are Poisson distributed with parameter equal to 6.
-
Knights (and queens)
(project)
students: Lea Micard, Eva Ragazzini, Lara Suys (report)
The gif is an animation of two movements of a knight on a chess board. The picture represents the number of jumps needed for the knight to reach every square on a torus-shaped chess board.


-
Magic squares of squares
(project)
students: Arjanita Dingu, Clara Duchossois (report)
The following visualisations are the result of some generalization of the concept of magic squares:
- Magic tetrahedron of sum 576
- Magic star of sum 630
- Magic Sierpinski tetrahedron of sum 1292



-
Music in Fibonacci numbers
(project)
students: Beatrice Bach, Loris Chenneaux (report)
The first audio file represents the Fibonacci sequence (mod 5) in the E minor Pentatonic scale. The second one corresponds to the A minor blues scale where we take the sequence mod 12.
-
Fractal limit sets and Schottky groups
(project)
students: Inas Bosch, Yanis Bosch (report)

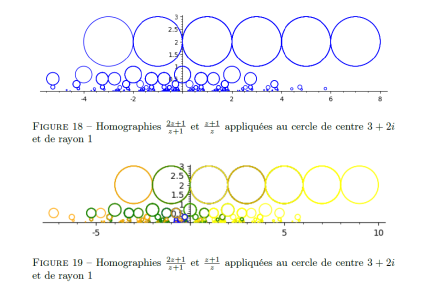
-
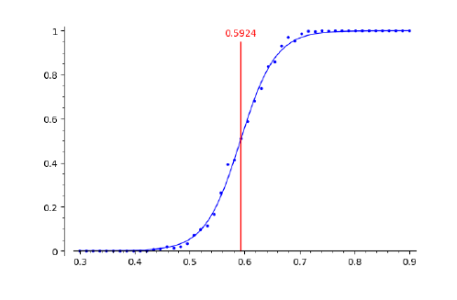
Percolation
(project)
student: Tim Seuré (report)
The first picture represents an $80\times80$ grid with open (blue) and closed (black) sites. We are interested in the length of the shortest path (if it exists) of blue sites that goes from top to bottom. You can see the shortest path in red and its length is 97. While this can be computed directly for a predetermined system of open and closed sites, it is an interesting research problem to study the behavior of the shortest path where sites are opened at random with some probability. In the second picture you can see the probability that there is a path of open sites from top to bottom as we increase the probability that a site is open.

-
Perturbations of the Lorenz system
(project)
students: Sven Federspiel, Alex Schammo
The first video represents the following situation: By changing the value $r$ of the equation with initial values $(10,10,10)$, we see that there is a range where the convergence to the positive or negative convergence points stays stable. It is quite surprising to have this form of stability in a complete chaos theoretic system of equations, and one is free to look for themselves where this might come from. The second video corresponds to the following: By changing the value $f$ of the periodic function, the stability of convergence is also modified. One can clearly see that the system switches from "nearly-lorenz" to "tornado-like" behaviour, which results in a very beautiful video.
-
Runs in random sequences
(project)
students: Yanis Bosch, Tim Seuré (report)
The first picture is a realization of a 1D symmetric random walk up to the first time it is at distance 5000 from the origin (it takes more than 35 million steps!). Then you can see 1000 symmetric random walks run in parallel (picture is rotated 90 degrees). The last picture presents a realization of a symmetric random walk in 2D with a color gradient corresponding to time. For more graphs, check out the project report.



-
Visualization of Bianchi fundamental polyhedra
student: Kelly Jost


-
Convex hulls of finite packs of spheres
student: Fabio Marcelo Carvalho dos Santos
The first picture shows a minimal sphere packing that is more efficient than the linear 3-dimensional sphere packing. The following five pictures are sphere packings obtained from the five platonic solids.