Lët'z box counting!
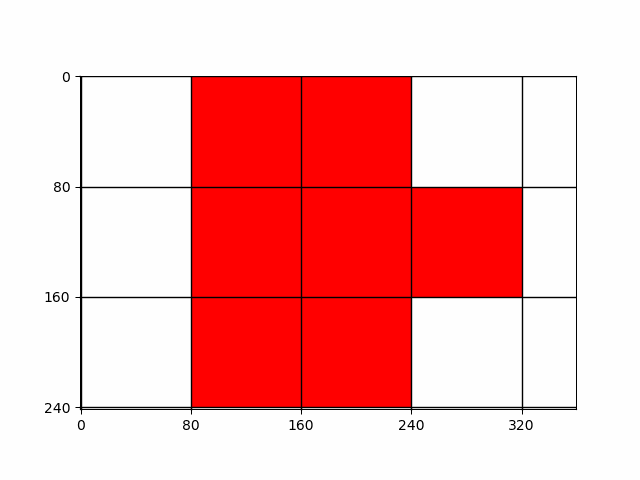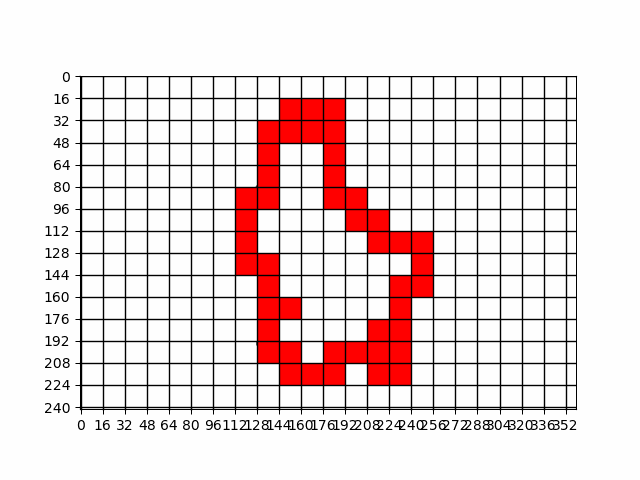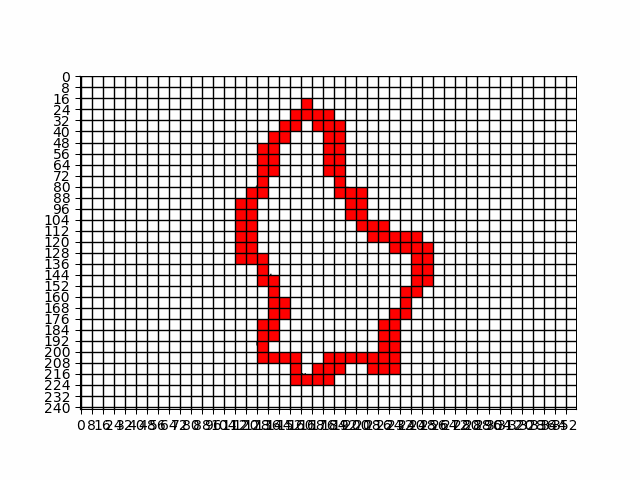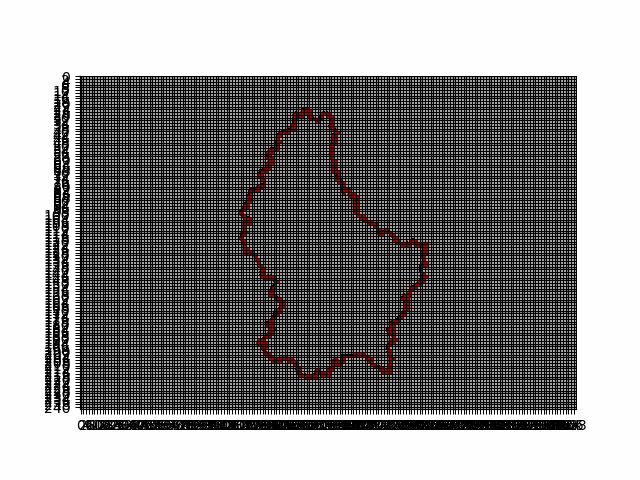

The box counting principle is a method used in fractal geometry to measure the complexity of a shape, such as the border of a country. To apply this method, imagine covering the map of Luxembourg or the UK with a grid of equally sized boxes. You then count how many boxes contain a part of the border.
Next, you repeat the process with smaller boxes, counting how many of these smaller boxes touch the border. As you keep reducing the box size and counting, you plot these counts on a graph with the box size on one axis and the number of boxes on the other axis.
For a regular shape, the relationship between box size and count is straightforward, but for complex, irregular borders, this relationship reveals a pattern. The way the number of boxes increases as their size decreases can help determine the fractal dimension of the border, a measure of its complexity.
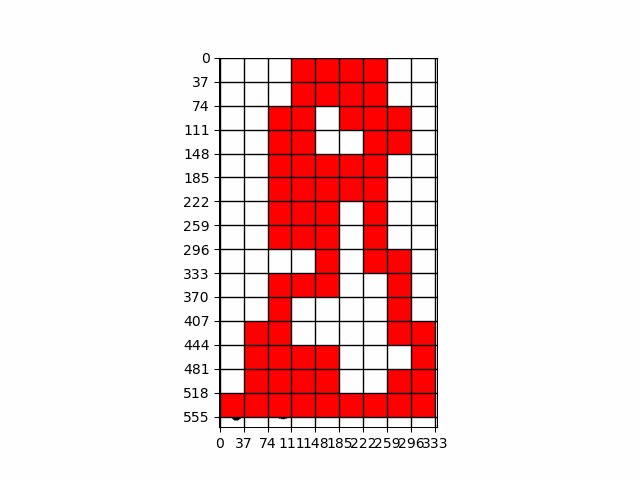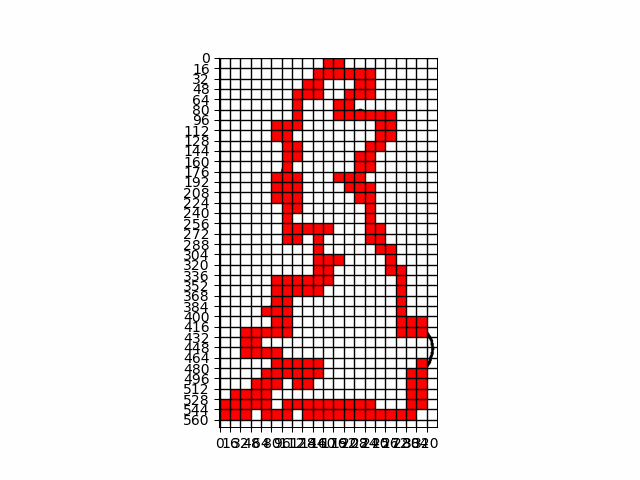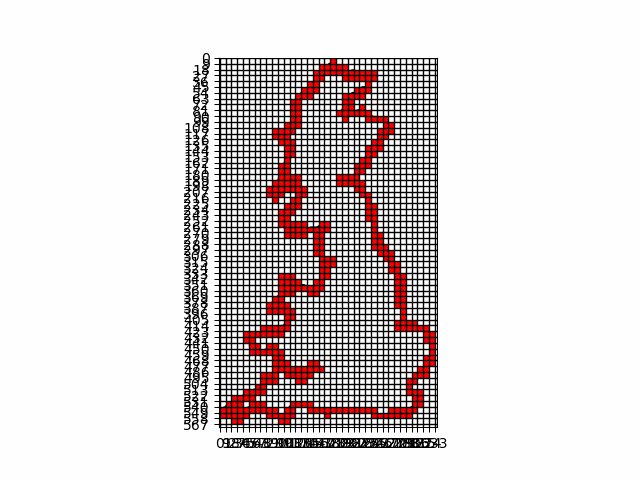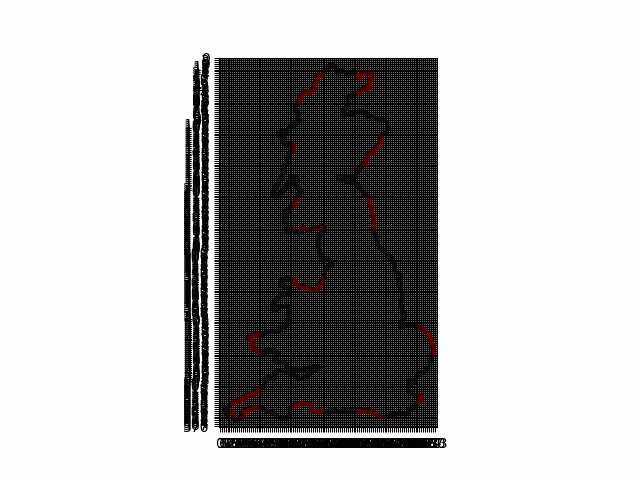
How is the box-counting dimension or the borders of Luxembourg (and UK)?
Luxembourg, being relatively small with a less convoluted border, might show a simpler pattern than the UK, which has a highly intricate coastline.
This method helps to quantify how 'fractal-like' a border is, capturing its complexity mathematically. The resulting fractal dimension is a non-integer that reflects how detailed the border is at different scales.
The box-counting dimension obtained for the borders of Luxembourg is 1.05 and for Great Britain coastline is 1.26! The first value is close to 1 (the fractal dimension of a circle is 1), which means that the borders of Luxembourg don't have a lot of deep edges.
Hence, this principle demonstrates that natural shapes often possess a fractal nature, exhibiting complexity beyond simple Euclidean geometry.
Credits: These animations were created as part of the Experimental Mathematics Lab project entitled ''Lët'z box counting'', which was the bachelor thesis of our student Kim Da Cruz, and was supervised by Dr. Guendalina Palmirotta and Dr. Lara Daw.
Further information: Check out the Bachelor thesis of Kim Da Cruz on our Experimental Mathematics Lab website.
Other languages:
Français Deutsch