Eye-catching patterns

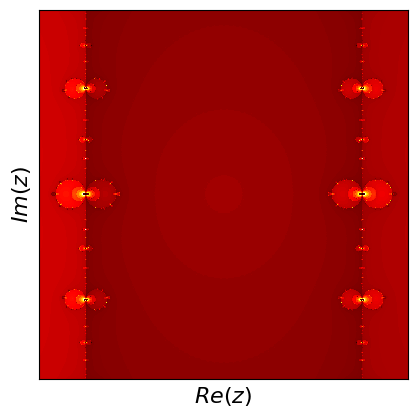
Newton fractals are a fascinating intersection of mathematics and art, created by applying Newton's method to find the roots of a complex polynomial function. Newton's method is an iterative process that starts with an initial guess and repeatedly applies a formula to get closer to a root. For complex polynomials, this method can be visualized in the complex plane, where each point represents a complex number. The color of each point indicates which root the method converges to when starting from that point, and how quickly it converges.
If you start at different points, the method can lead to different roots, and this creates a beautiful, intricate pattern known as a fractal. Fractals are patterns that repeat at different scales, displaying self-similarity. The boundaries between regions converging to different roots are incredibly complex and infinitely detailed. These boundaries are where the fractal nature is most evident, showcasing infinitely repeating patterns no matter how closely you zoom in. Newton fractals illustrate both the power of Newton's method and the intricate beauty of mathematical chaos and complexity.

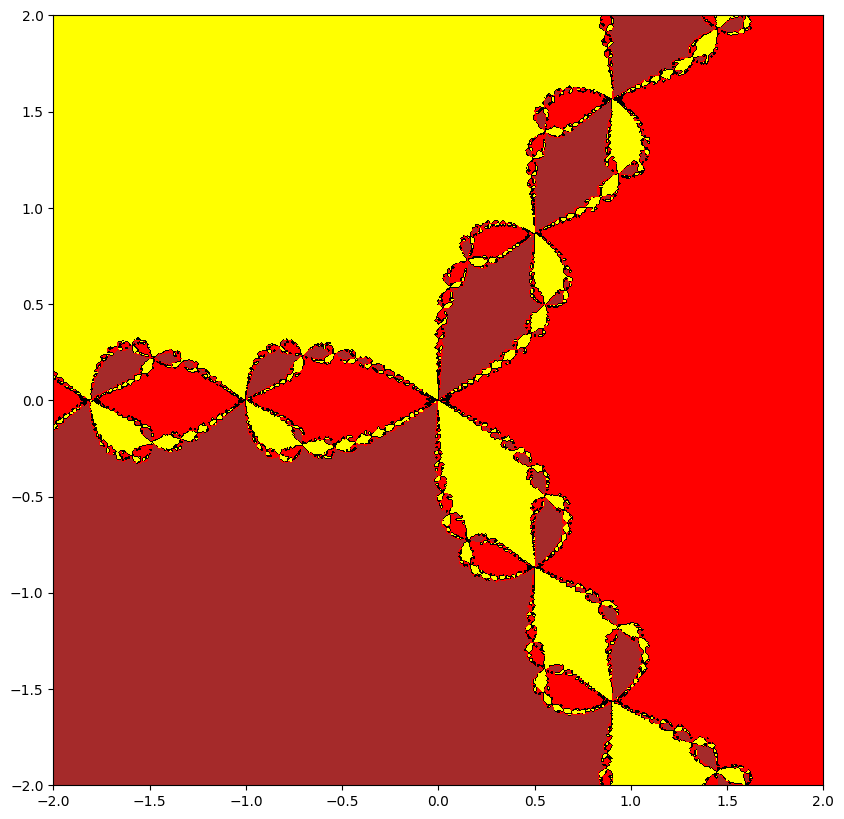
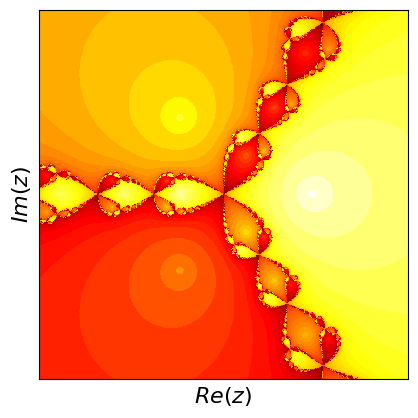
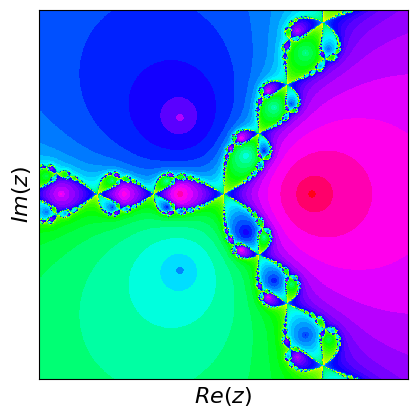
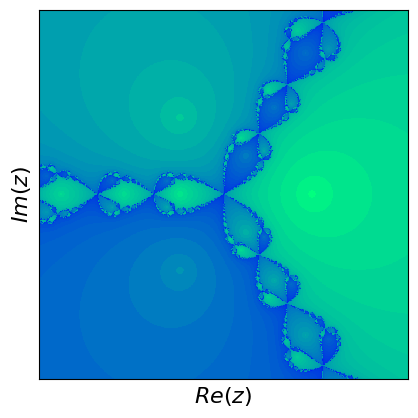
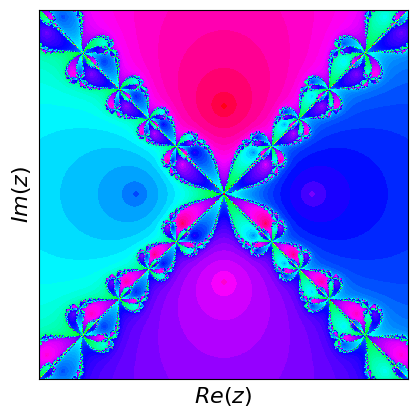
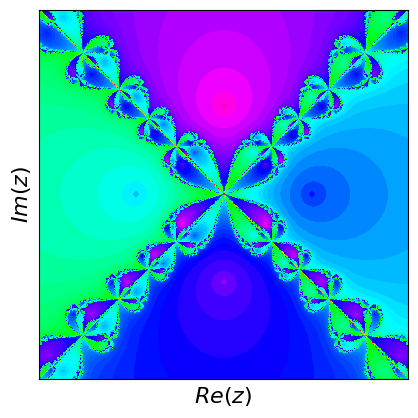
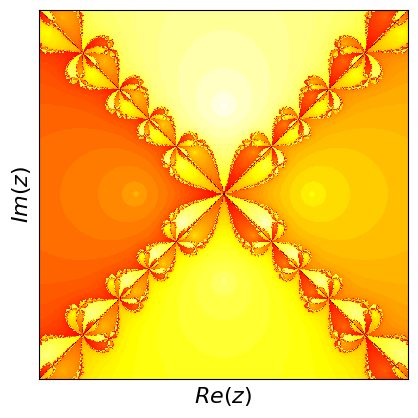
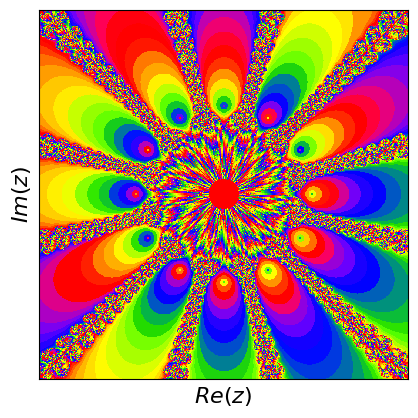
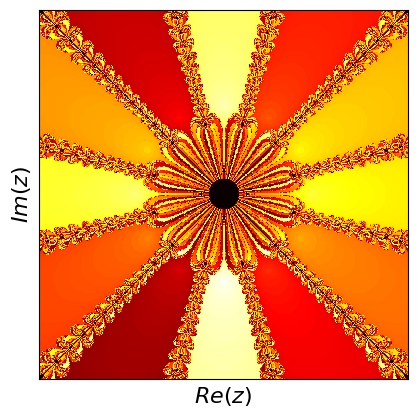
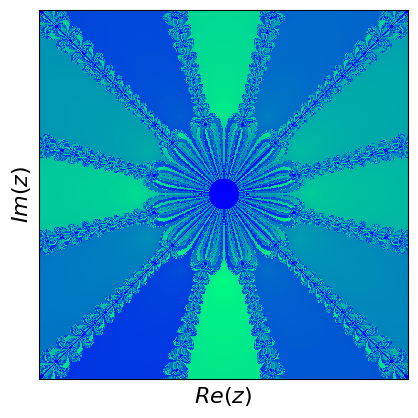
$Newton fractals 33$ $Newton fractals 32$ $Newton fractals 33$ $Newton fractals 6$ $Newton fractals 7$ $Newton fractals 8$ $Newton fractals 10$ $Newton fractals 28$ $Newton fractals 14$ $Newton fractals 16$ $Newton fractals 19$ $Newton fractals 2$ $Newton fractals 3$ $Newton fractals 25$ $Newton fractals 12$ $Newton fractals 31$ $Newton fractals 18$ $Newton fractals 13$ $Newton fractals 17$ $Newton fractals 1$ $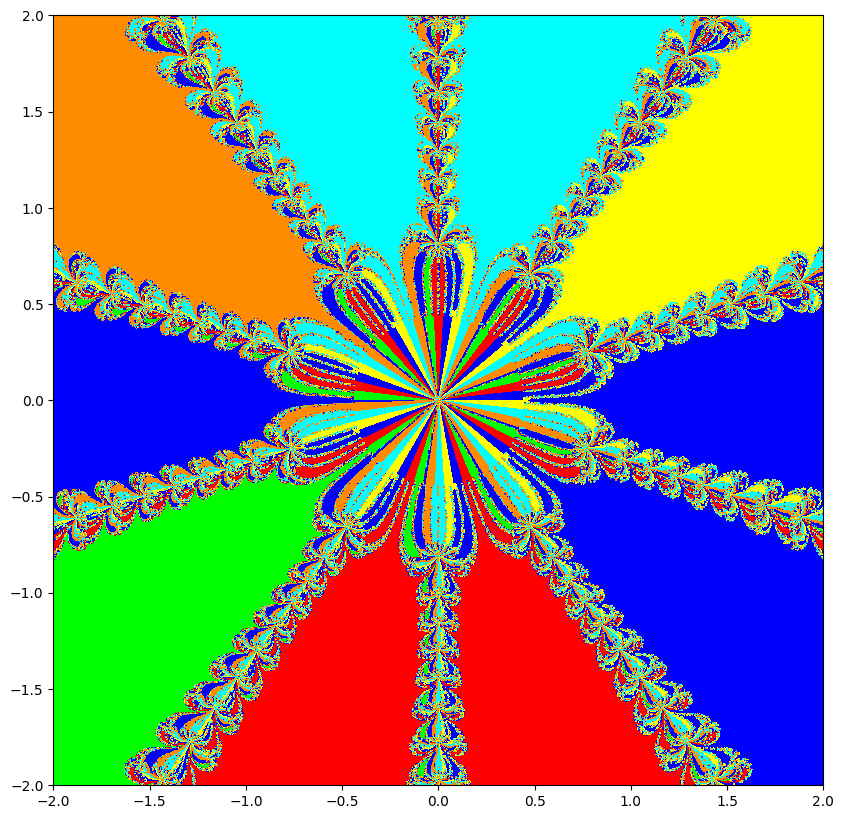Newton fractals 4$ $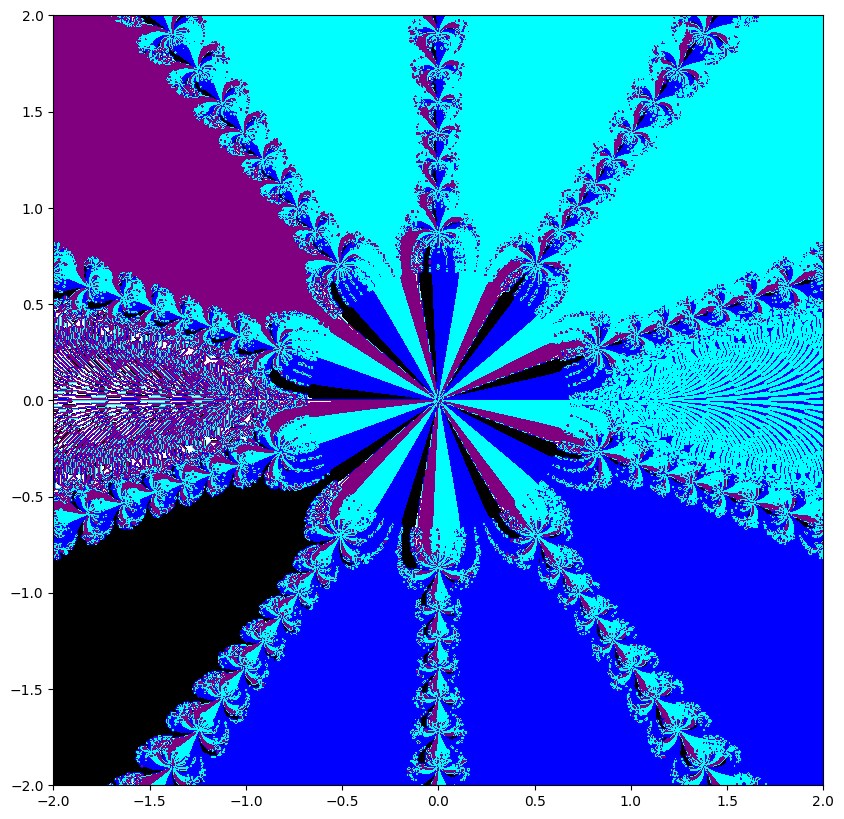Newton fractals 5$ $Newton fractals 11$ $Newton fractals 27$ $Newton fractals 26$ $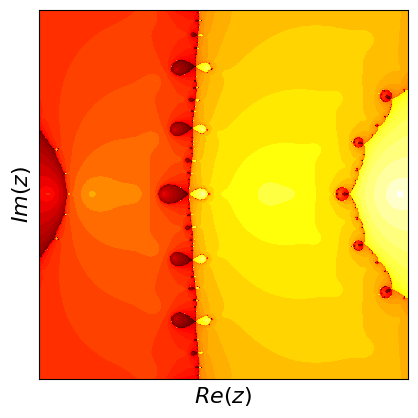Newton fractals 20$ $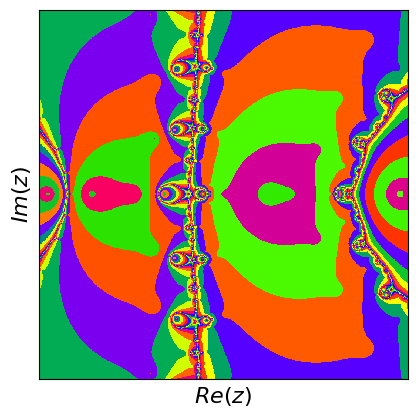Newton fractals 21$ $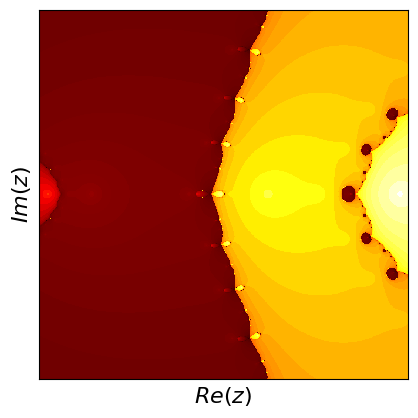Newton fractals 22$ $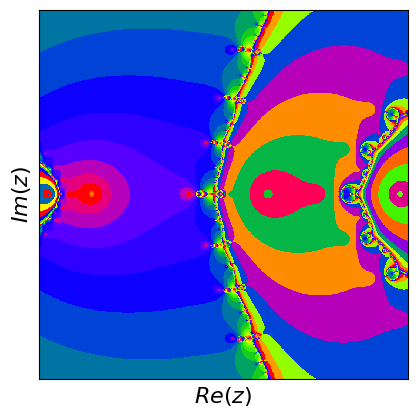Newton fractals 23$ $Newton fractals 24$ $Newton fractals 29$ $Newton fractals 30$

What are fractals? Fractals are complex geometric shapes that can be split into parts, each of which is a smaller, self-similar copy of the whole. They exhibit patterns that repeat at every scale, meaning no matter how much you zoom in, you'll see the same type of pattern. Examples include natural forms like snowflakes, mountain ranges, and broccoli, as well as mathematical constructs like the Mandelbrot set.

Credits: These images were created in the Experimental Mathematics Lab by Dr. Guendalina Palmirotta.

Further information: Check out "Fractals derived from Newton-Raphson iteration", "The Quest to Decode the Mandelbrot Set, Math’s Famed Fractal" and the video for more explication.

Other languages:

Français Deutsch