Bizarre fireballs

en

  Symmetry is all about balance and harmony, and it's everywhere around us. Think about a butterfly's wings, they are perfectly balanced on both sides, like a mirror image. Flowers have symmetrical petals, each one mirroring the others around it. And if you look up at the stars, you'll see galaxies spinning in a symmetric way. There is symmetry everywhere: in art, in nature, and even within our bodies! Have you ever seen a building with perfectly matched windows on each side? That's symmetry at work. Artists love symmetry too. They use it to create beautiful patterns and designs. Even kids are confronted with symmetric art from a young age on when drawing a mandala or a butterfly. Artists use symmetry to make their compositions feel ordered and balanced. But symmetry isn't just for art—it's in science too. Scientists use symmetry to understand the world around us. They use math to describe how things move and change, and symmetry helps them see patterns and connections.

Animation hot roots Animation roots Animation zoom roots


But what exactly is symmetry?
Symmetry embodies the idea that certain transformations, such as reflection (happens when putting a mirror on the body of a butterfly), rotation (like turning the image of a sun), or translation (which is present in a honeycomb), leave an object unchanged or invariant, revealing fundamental patterns and relationships.

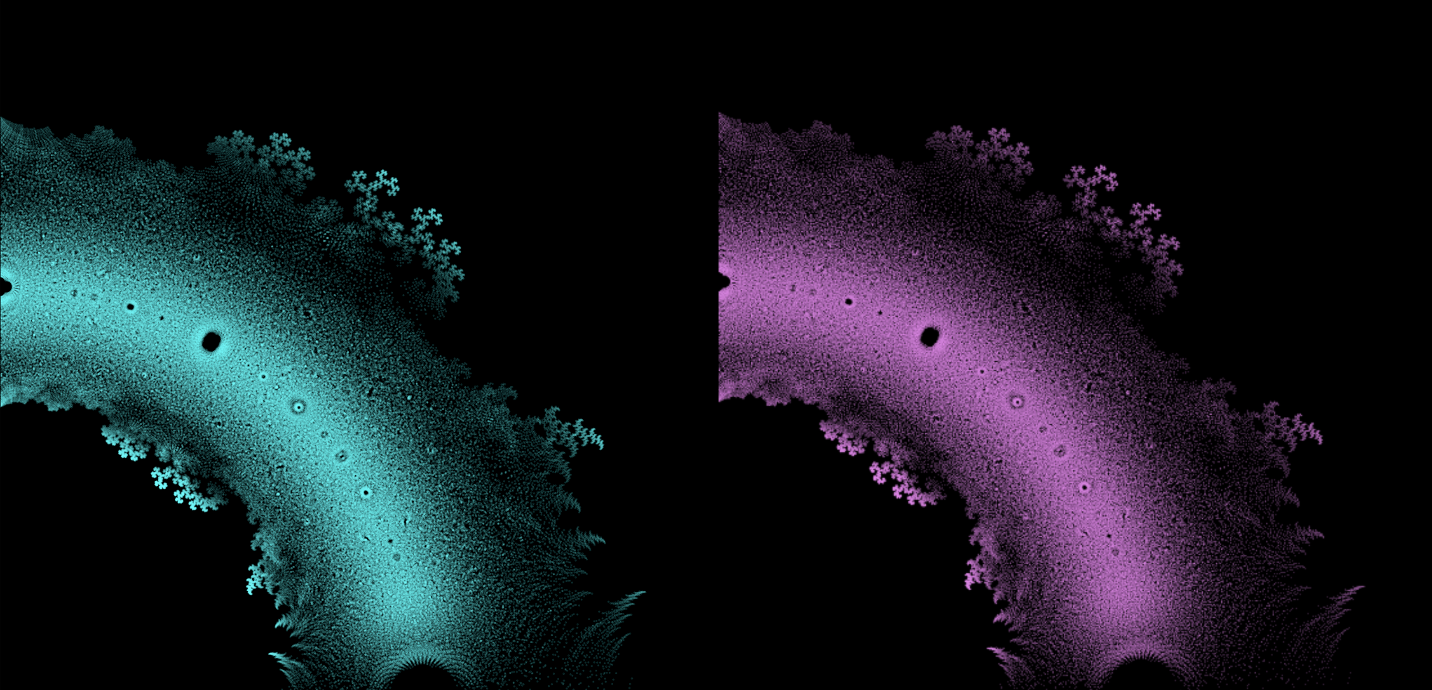
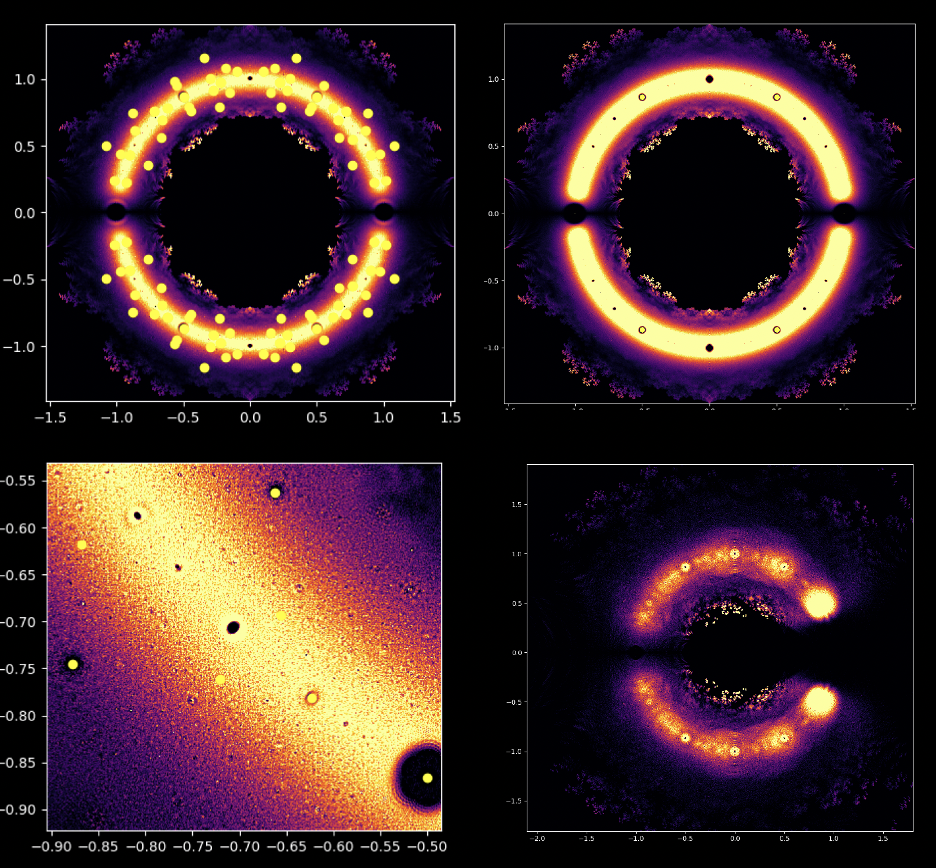
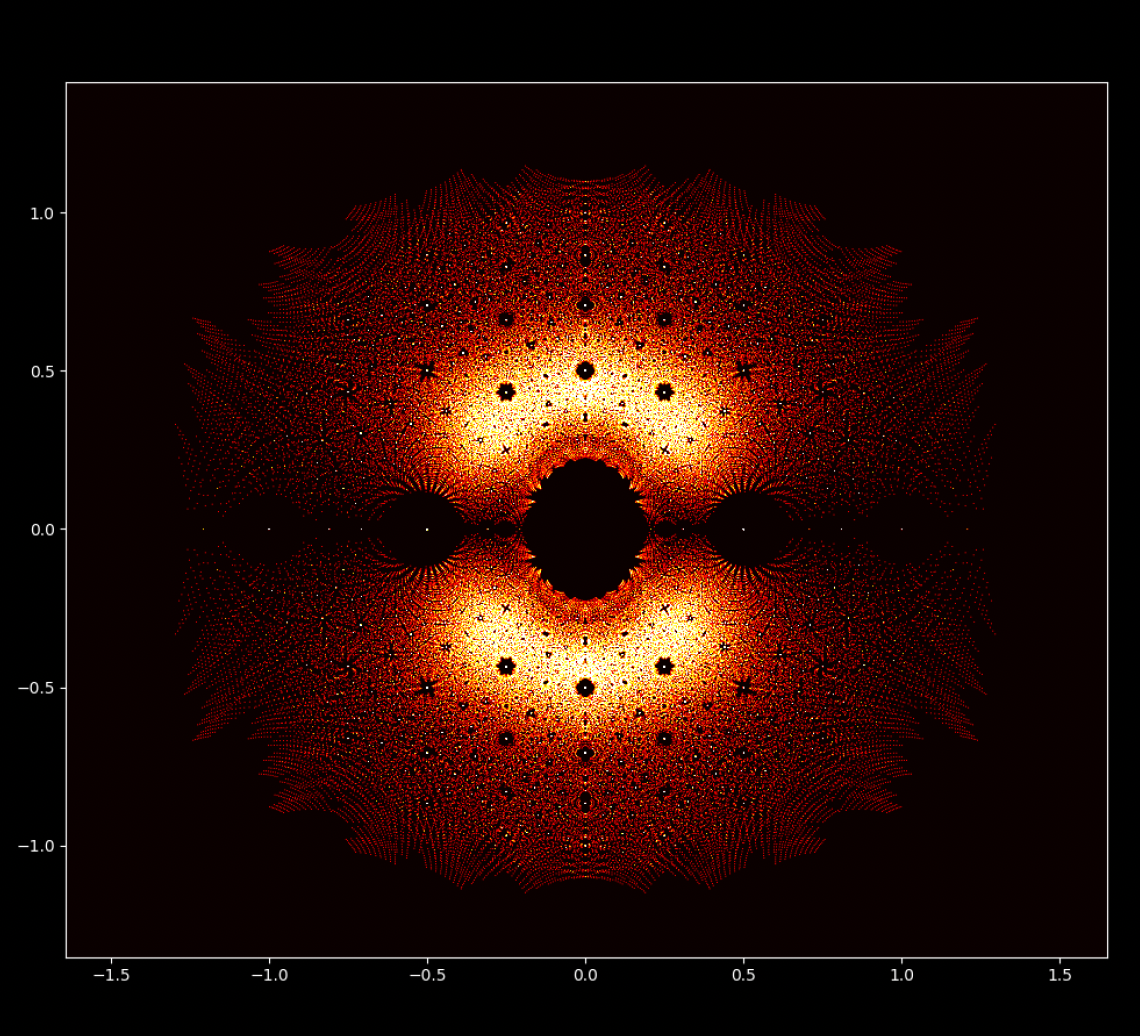
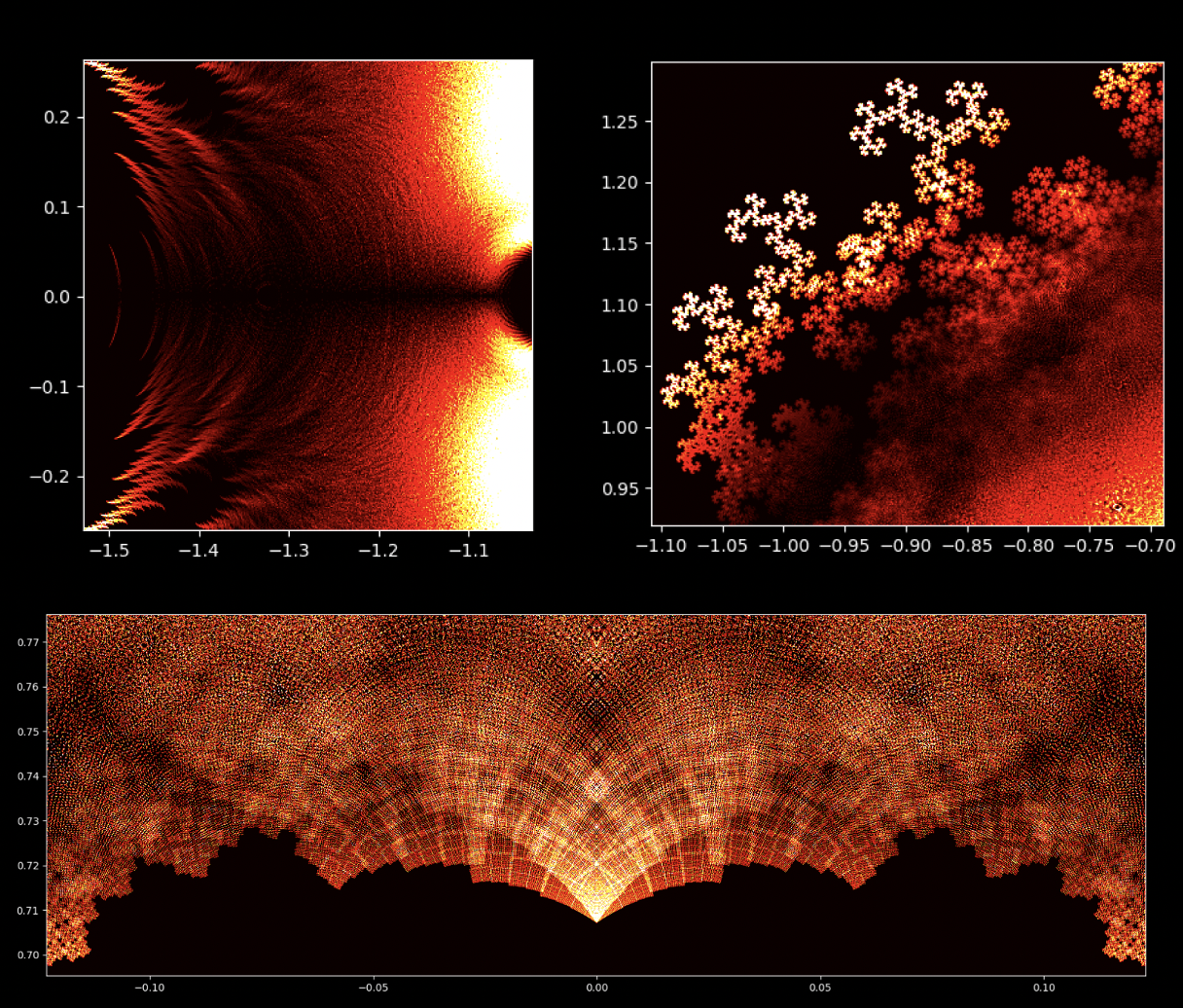
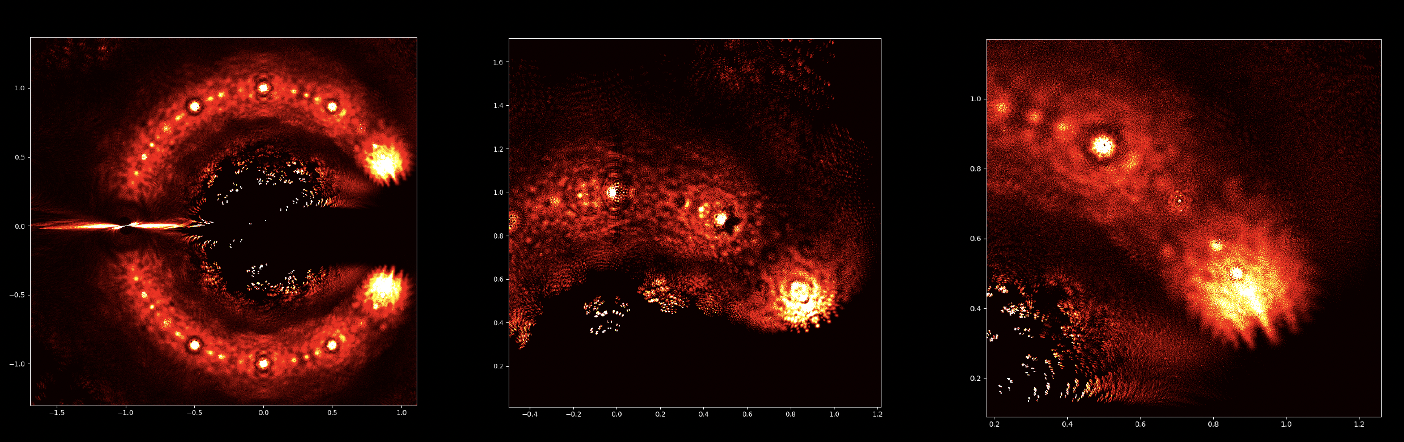
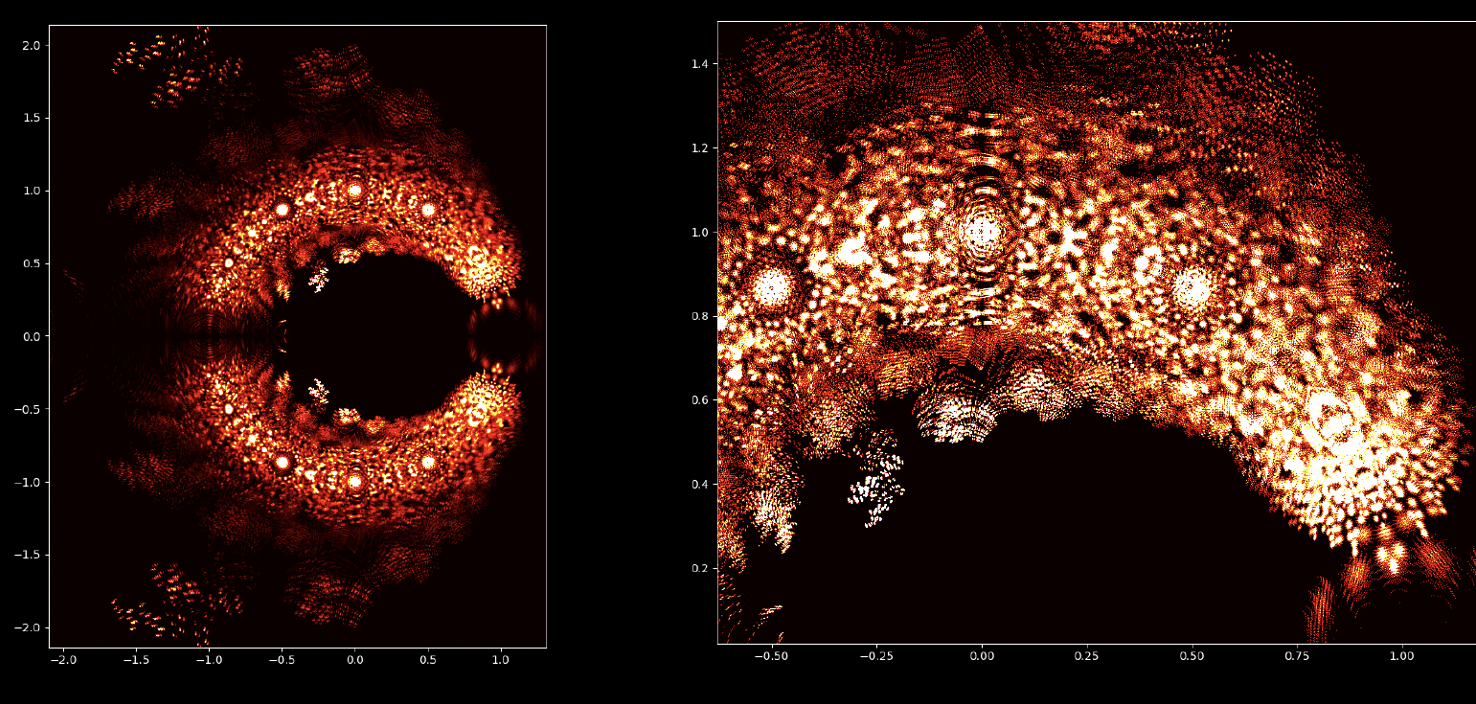
Coloured roots Zoom on the roots Flash roots Fireworks roots Fractals Fire roots Roots that look like worms


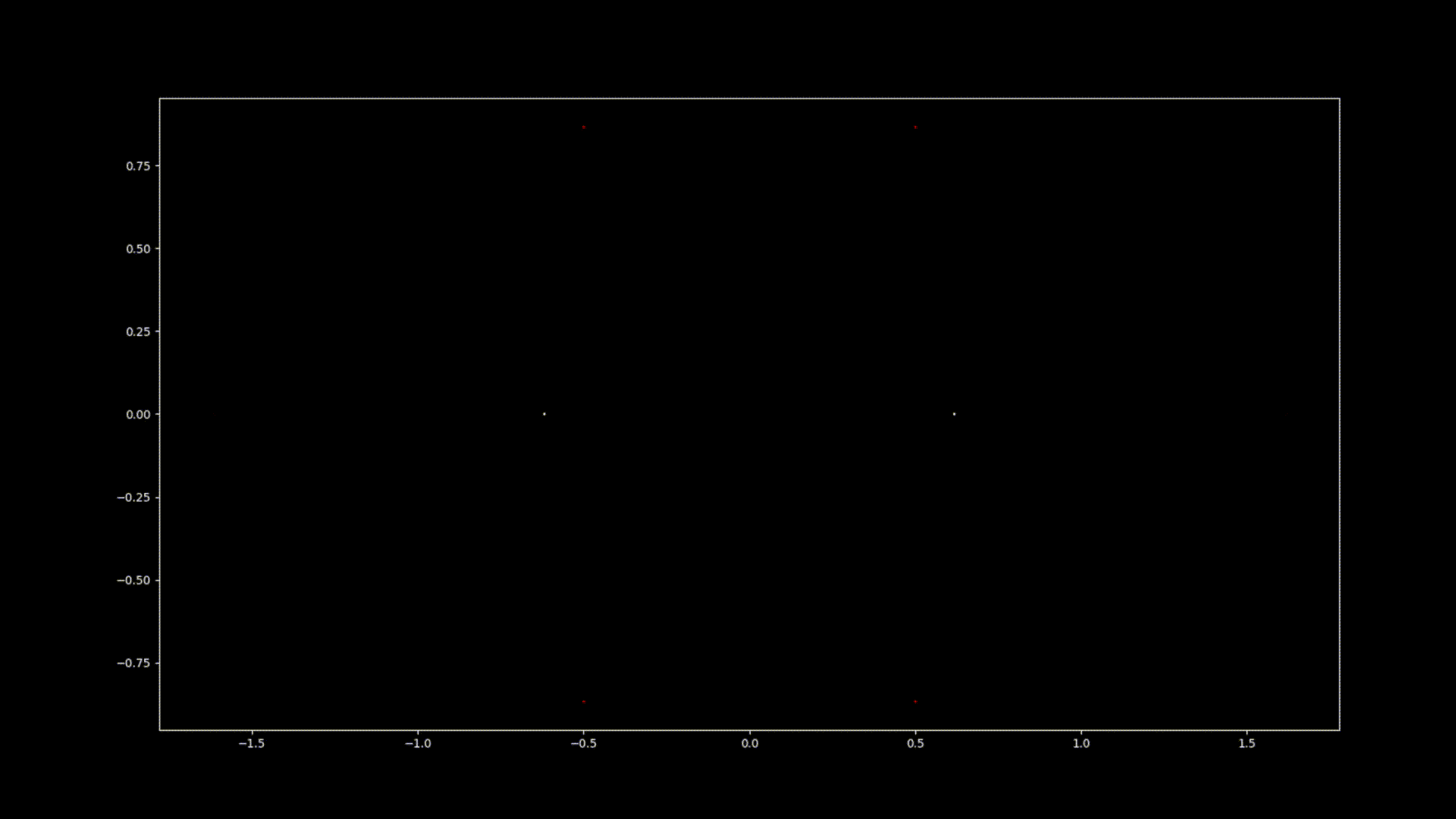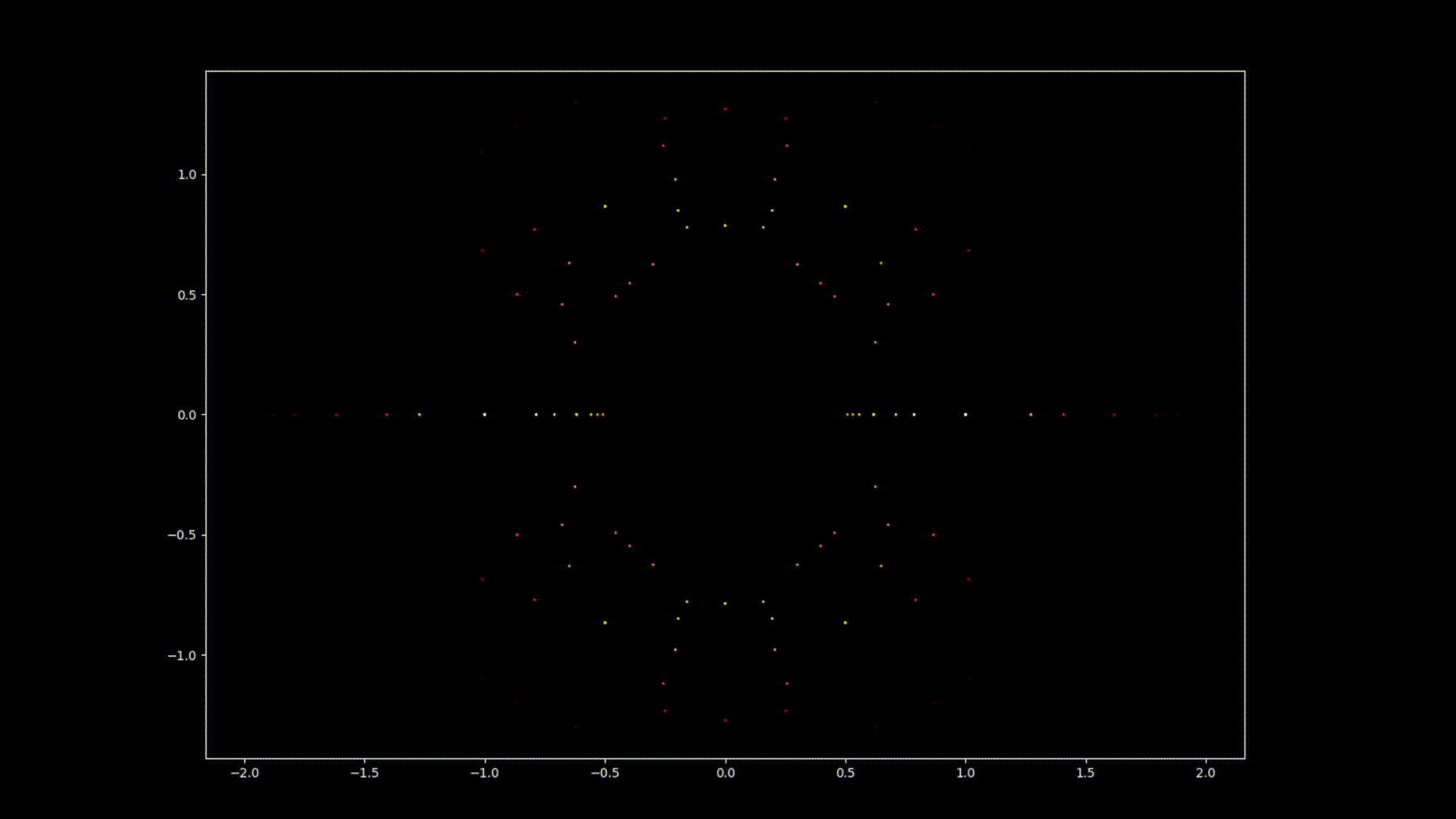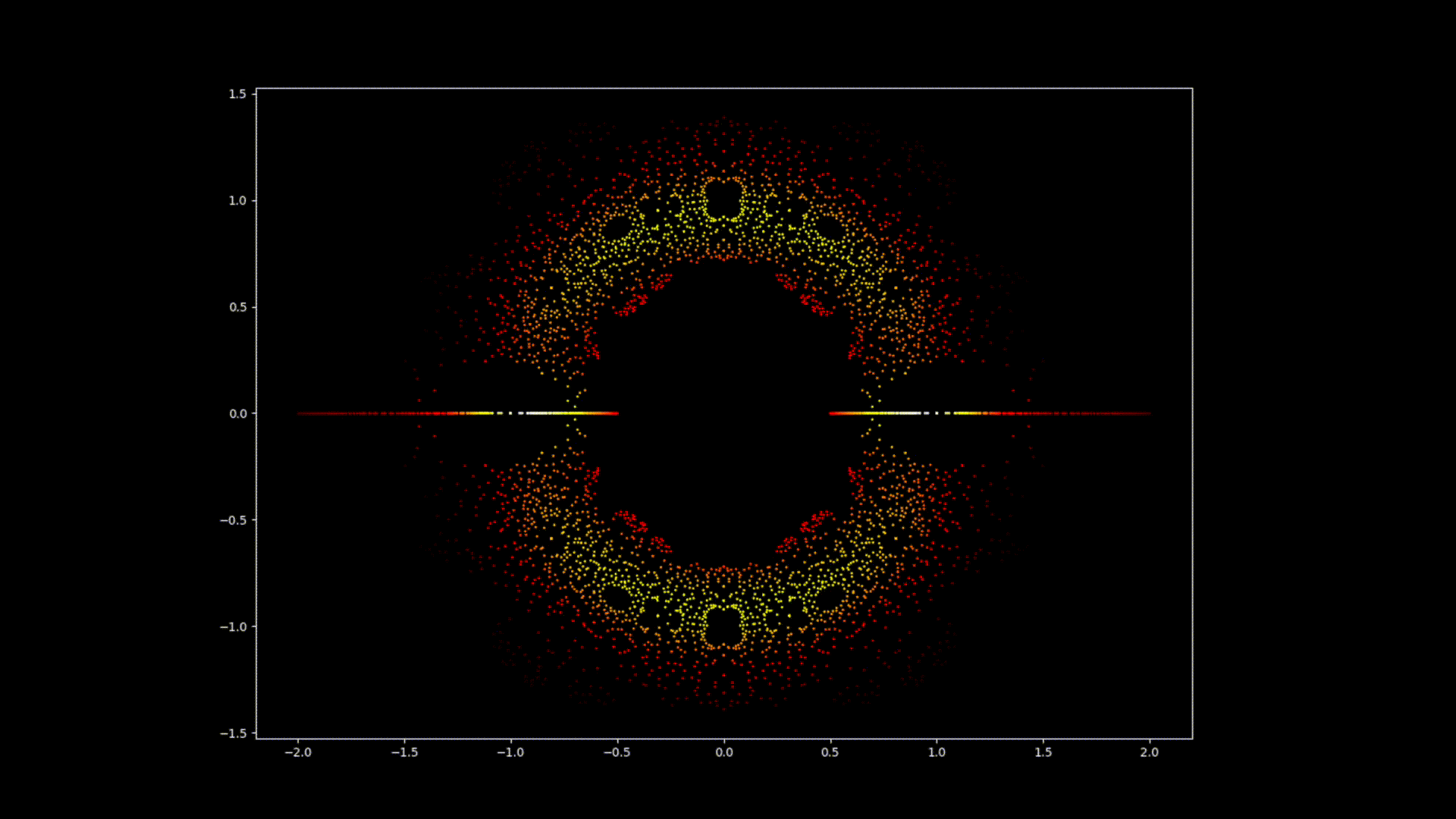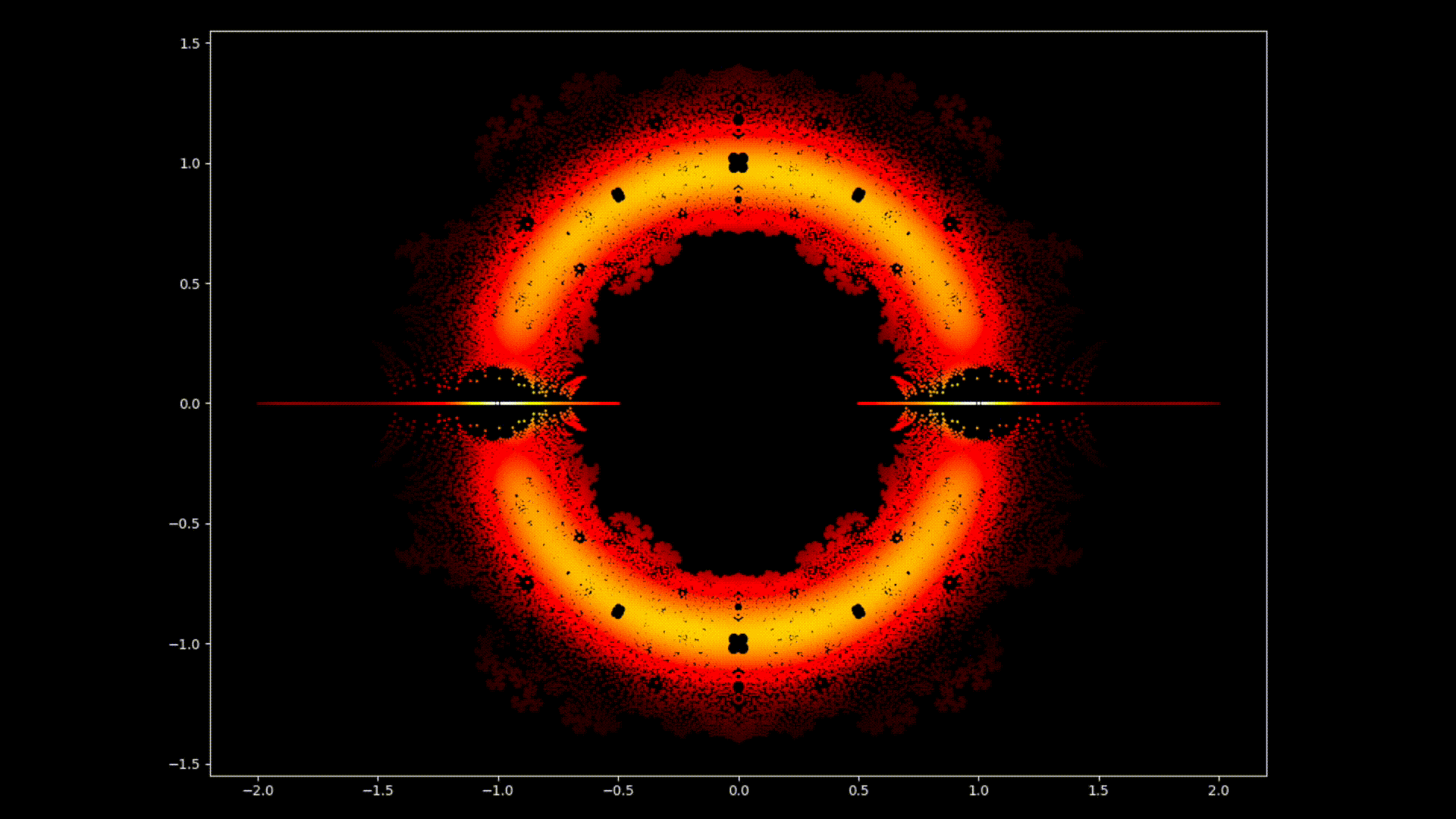
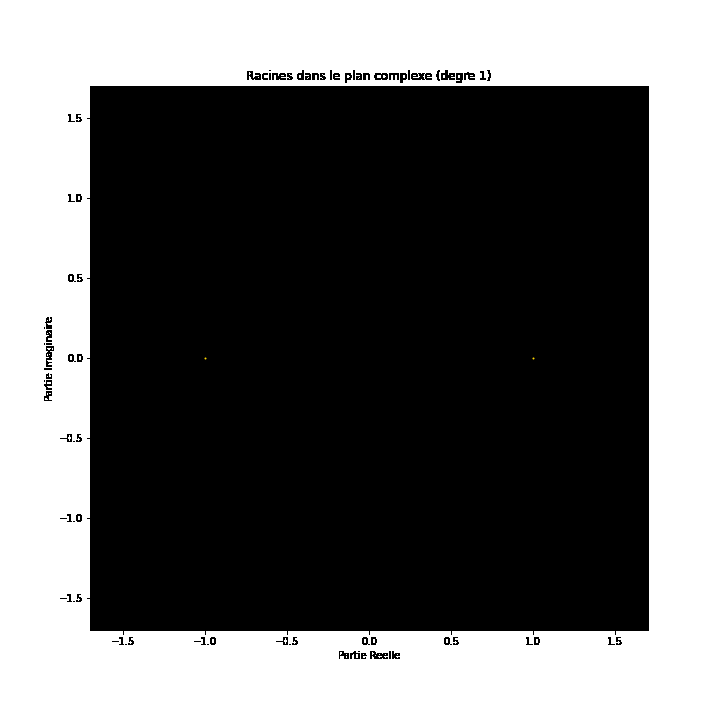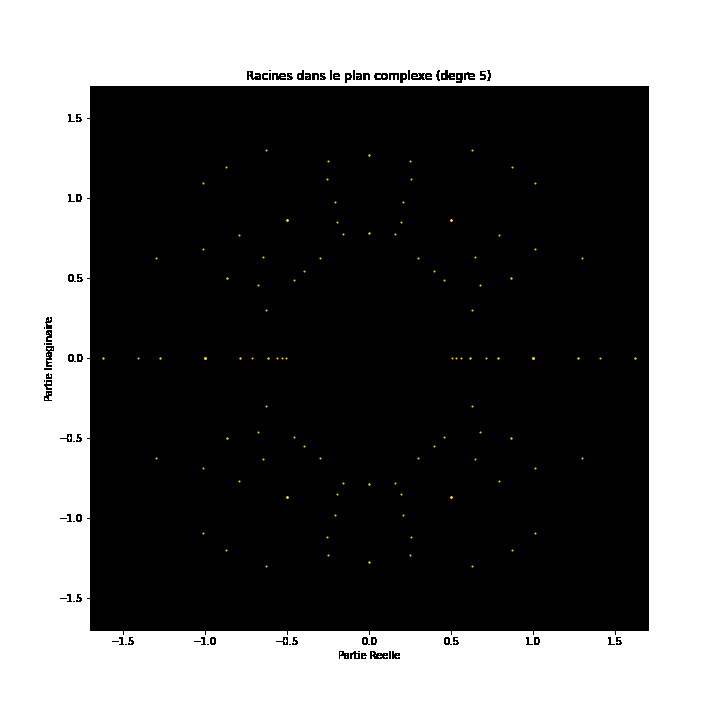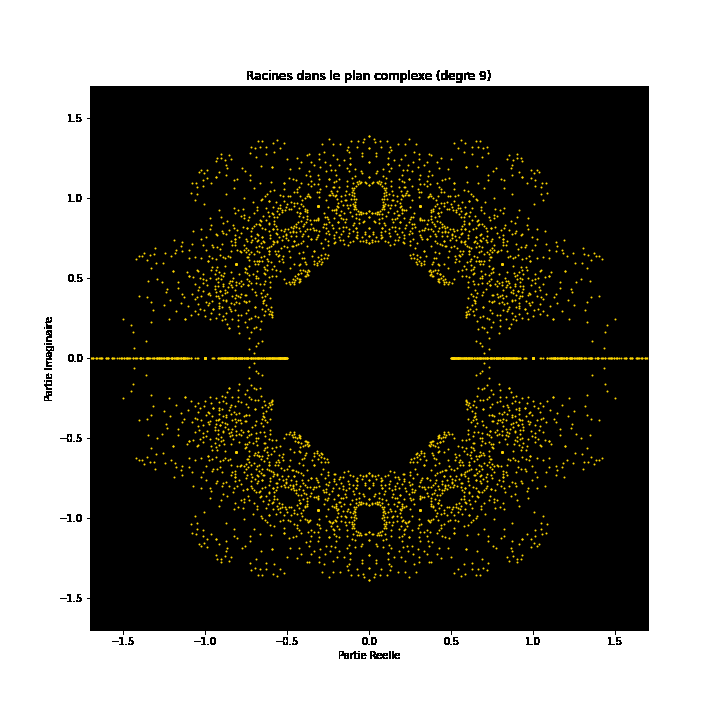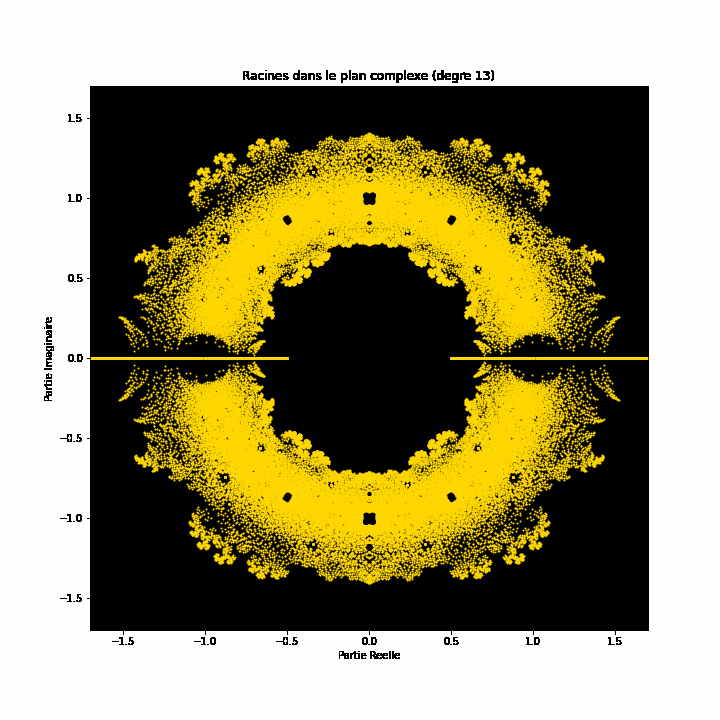
At first glance, polynomial equations may seem like abstract constructs, strings of numbers and variables arranged in a seemingly arbitrary way. However, under this surface lies a hidden order, a symmetrical harmony waiting to be discovered. The solutions of an equation, known as the roots or zeroes of the polynomial, hold a deep connection to the concept of symmetry. This symmetry can also be observed in the images of this EML project, in which we can observe the roots of polynomials with coefficients 1 and -1, which are visualised on the complex plane in a symmetric way, by plotting a point for each root. Real roots appear on the horizontal axis and complex roots on the vertical axis. We cannot see the single points plotted for each root as there are too many. In fact, there are 805.306.368 roots for a polynomial of degree 24, which all together form a bizarre fireball. These visual representations provide insights into the distribution, symmetry, and behaviour of the polynomial roots, helping us understand their properties and relationships, but they also show how beautiful Mathematics can be.

Credits: These images were created as part of the Experimental Mathematics Lab project entitled ''Visualising roots of algebraic numbers'', which involved many students, namely Claudia Marichal, Catia Alves Piro, Salma Belmir, Mikala Eisen, Melissa Genoud, Lynn Hellenbrand, Tom Kasel, Christophe Thelen, Gil Moes and Mirza Muharemovic, and was supervised by Prof. Gabor Wiese, Dr. Guendalina Palmirotta and Dr. Thierry Meyrath.

Further information: Check out John Baez's website "The beauty of roots" and our Experimental Mathematics Lab website.

Other languages: