Bizarre fireballs

de

  Symmetrie ist der Inbegriff von Balance und Harmonie und ist überall um uns herum. Denken Sie an die Flügel eines Schmetterlings: perfekt ausbalanciert und die eine Seite ist wie ein Spiegelbild der Anderen. Auch Blumen haben symmetrische Blütenblätter, da sich jedes Blatt im nächsten wiedergespiegelt ist. Und wenn Sie zu den Sternen aufblicken, sehen Sie Galaxien, die sich auf symmetrische Weise drehen. Symmetrie ist überall: in der Kunst, in der Natur und sogar in unseren Körpern! Haben Sie schon einmal ein Gebäude mit perfekt passenden Fenstern auf jeder Seite gesehen? Das ist Symmetrie in Aktion. Auch Künstler lieben Symmetrie. Sie nutzen sie, um schöne Muster und Designs zu kreieren. Selbst Kinder werden bereits in jungen Jahren mit symmetrischer Kunst konfrontiert, wenn sie ein Mandala oder einen Schmetterling zeichnen. Und in Gemälden verwenden Künstler Symmetrie, um ihren Kompositionen ein Gefühl von Ordnung und Balance zu verleihen. Aber Symmetrie ist nicht nur in der Kunst zu finden, sondern auch in der Wissenschaft. Wissenschaftler nutzen diese Symmetrie, um die Welt um uns herum zu verstehen. Sie verwenden Mathematik um zu beschreiben wie sich Dinge bewegen und verändern. Die Symmetrie hilft ihnen, Muster und Verbindungen zu erkennen.

Animation hot roots Animation roots Animation zoom roots


Aber was genau ist Symmetrie?
Symmetrie verkörpert die Idee, dass bestimmte Transformationen, wie zum Beispiel Spiegelung (wie das Einsetzen eines Spiegels in die Mitte eines Schmetterlings), Rotation (wie das Drehen des Bildes einer Sonne) oder Translation (die in einem Bienenstock vorhanden ist), ein Objekt unverändert oder invariant lassen und dabei grundlegende Muster und Beziehungen offenbaren.

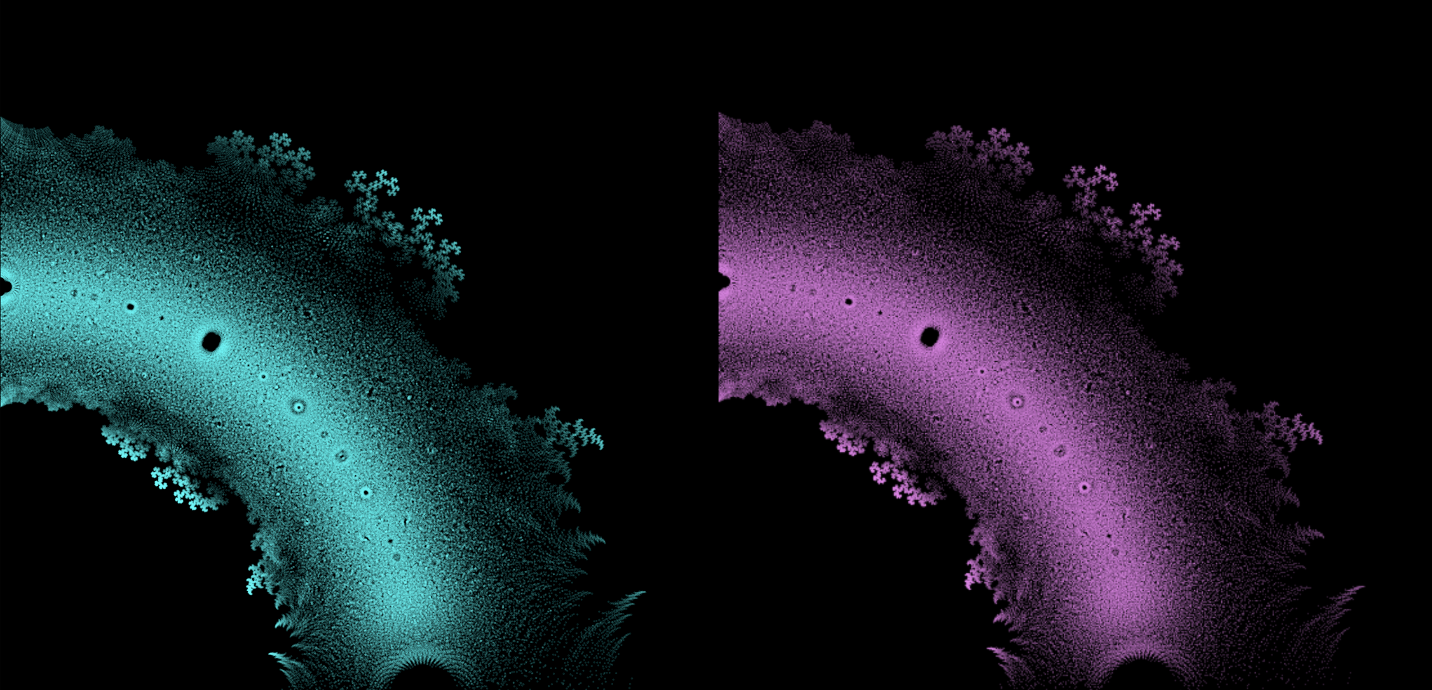
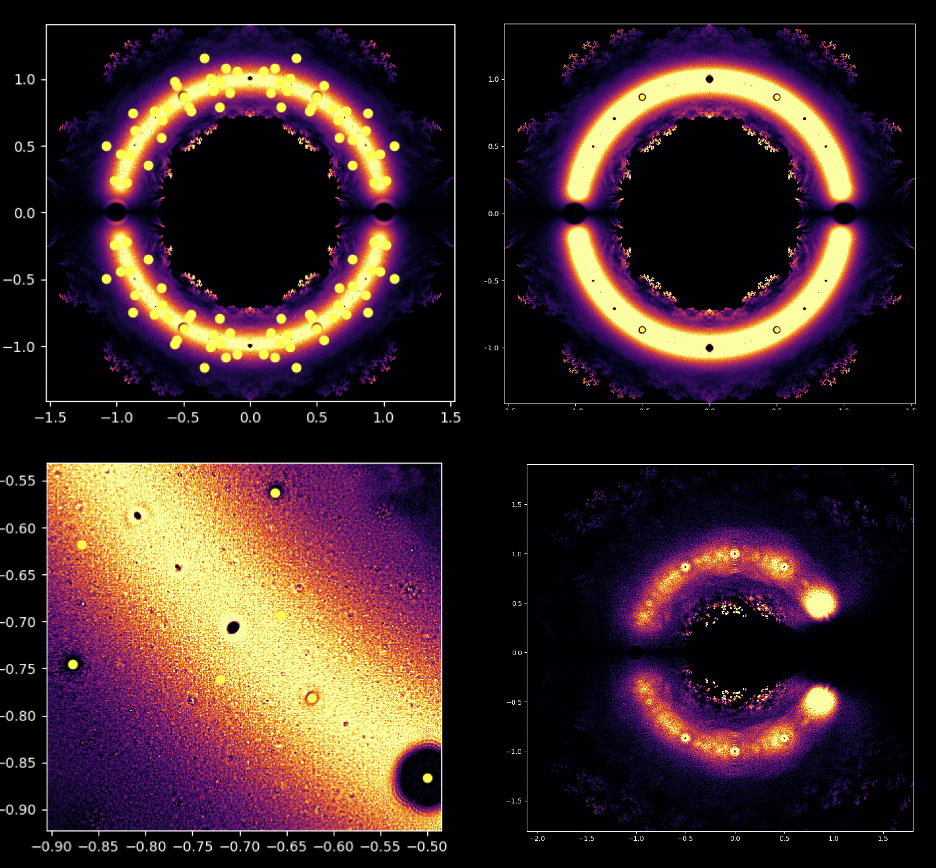
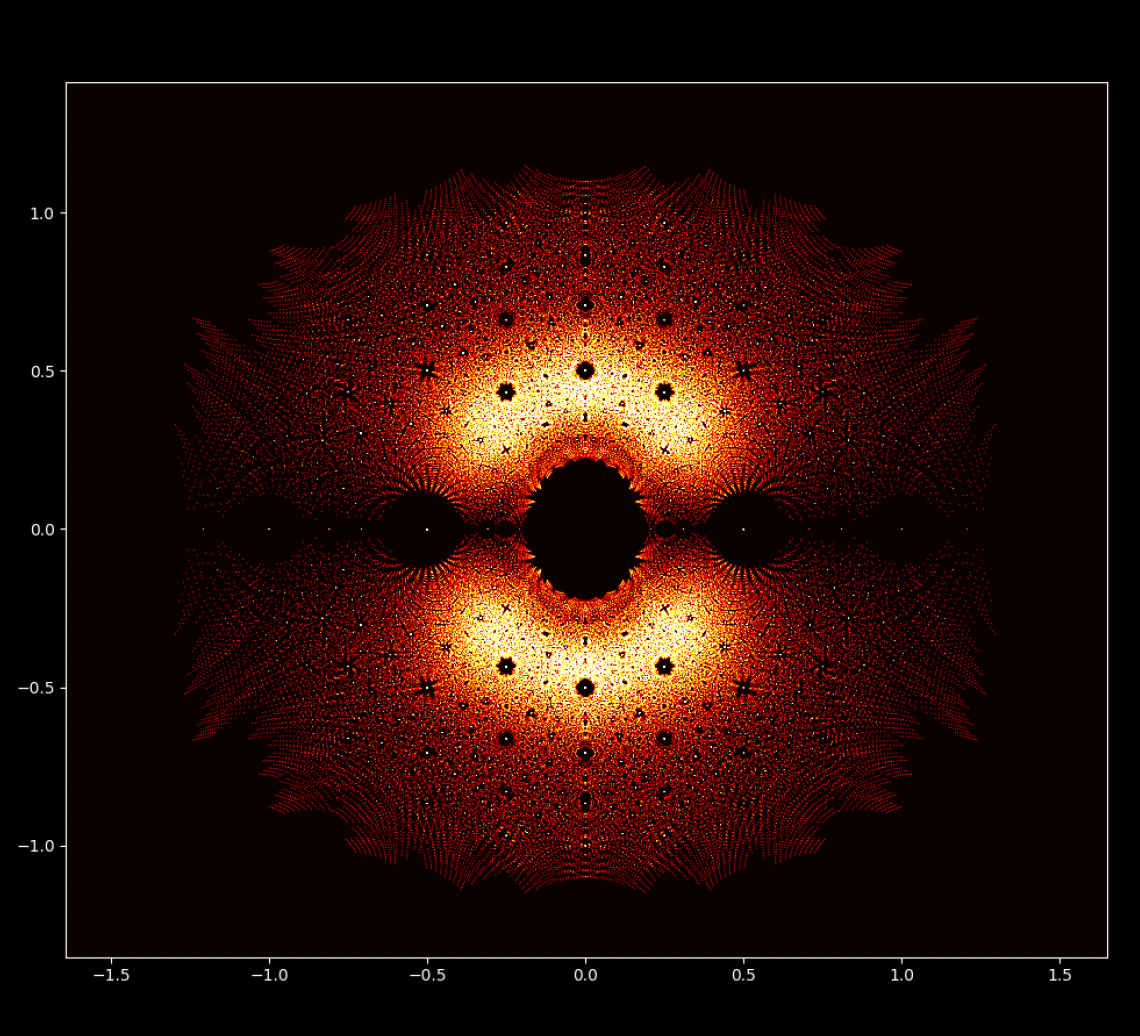
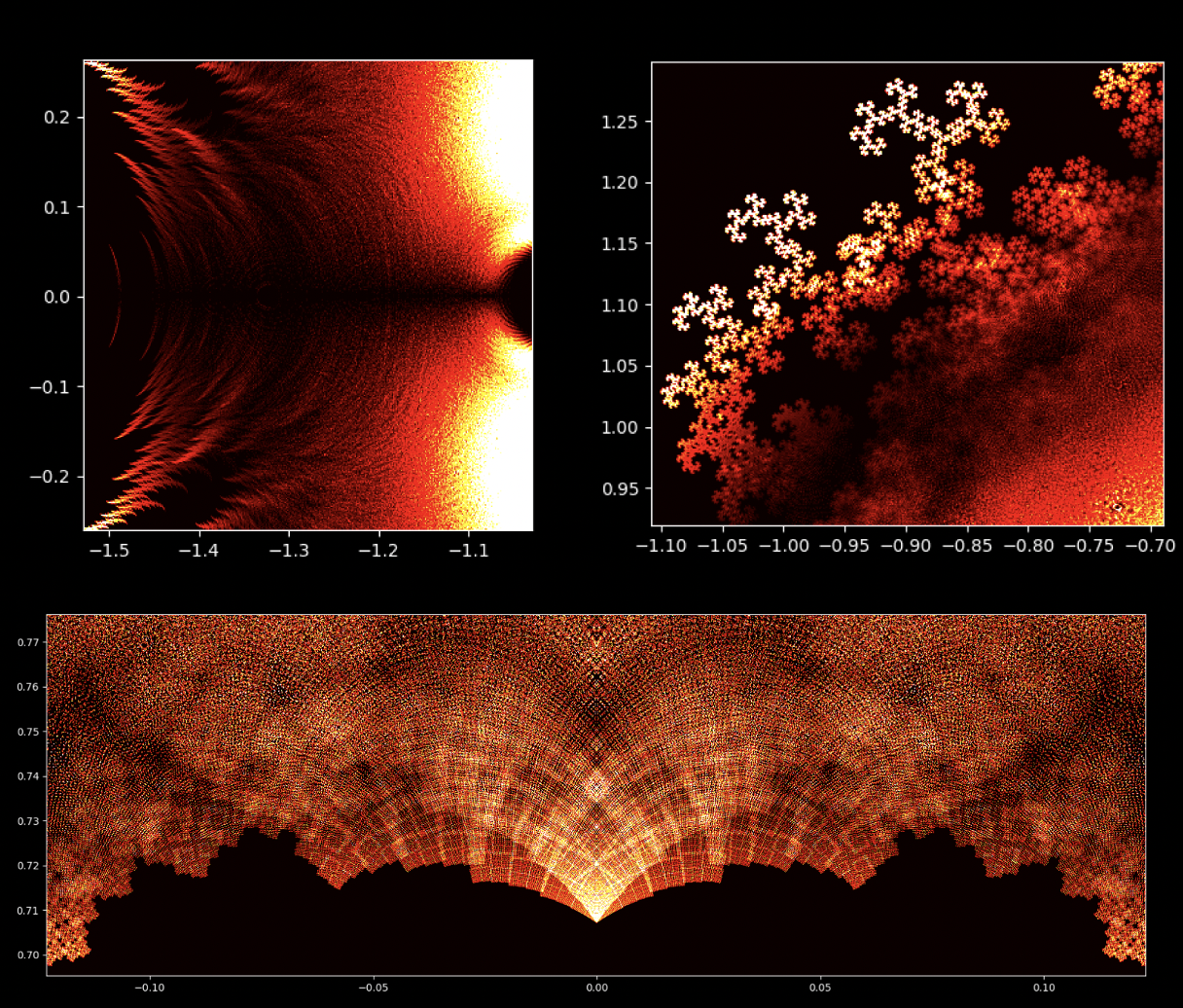
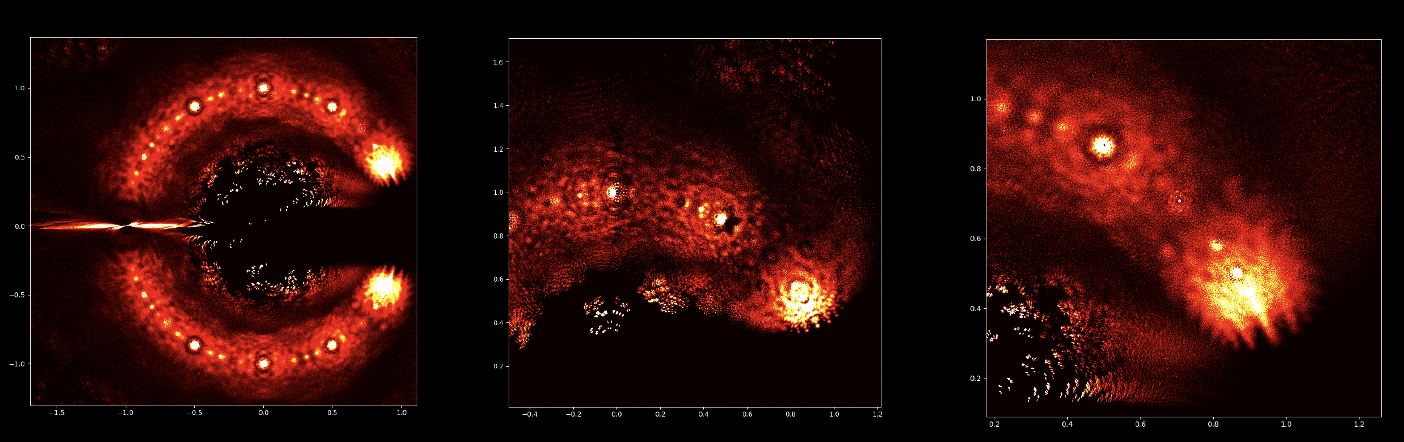
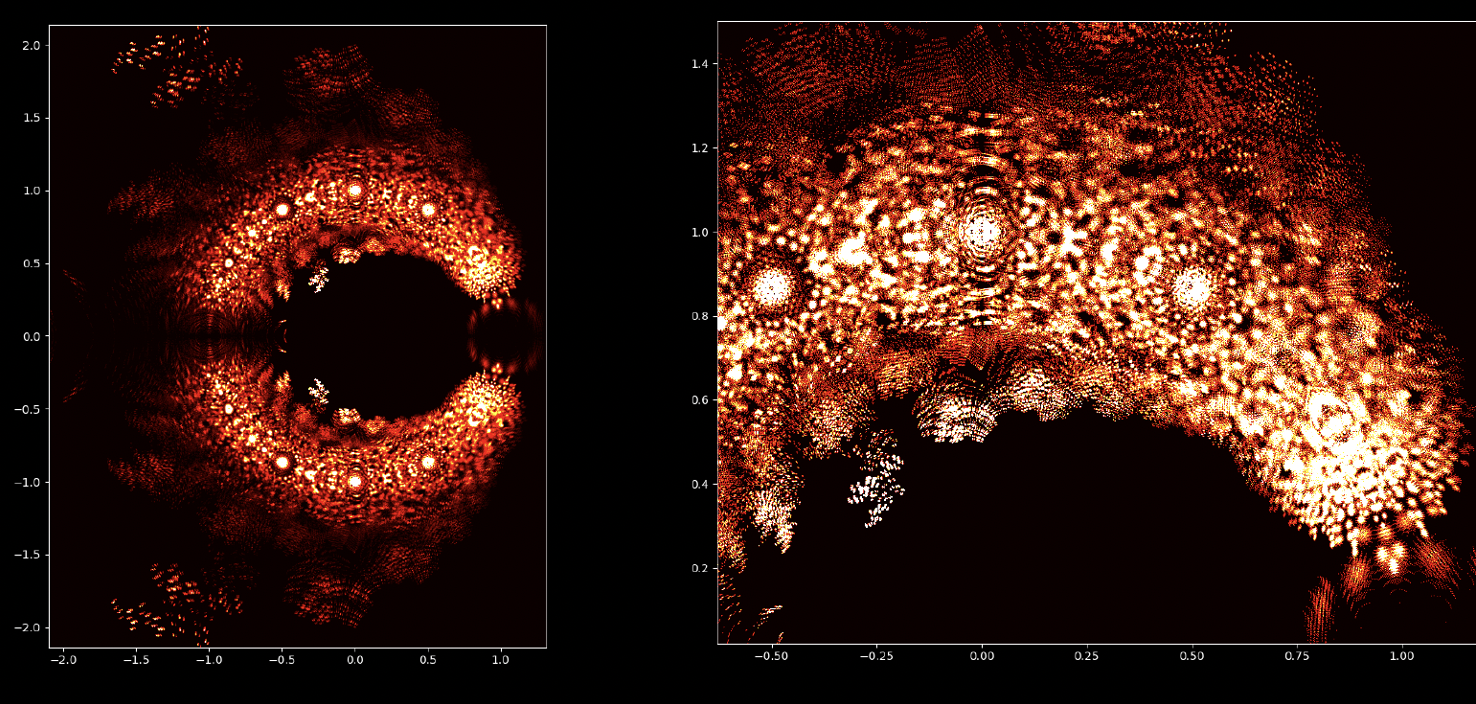
Coloured roots Zoom on the roots Flash roots Fireworks roots Fractals Fire roots Roots that look like worms


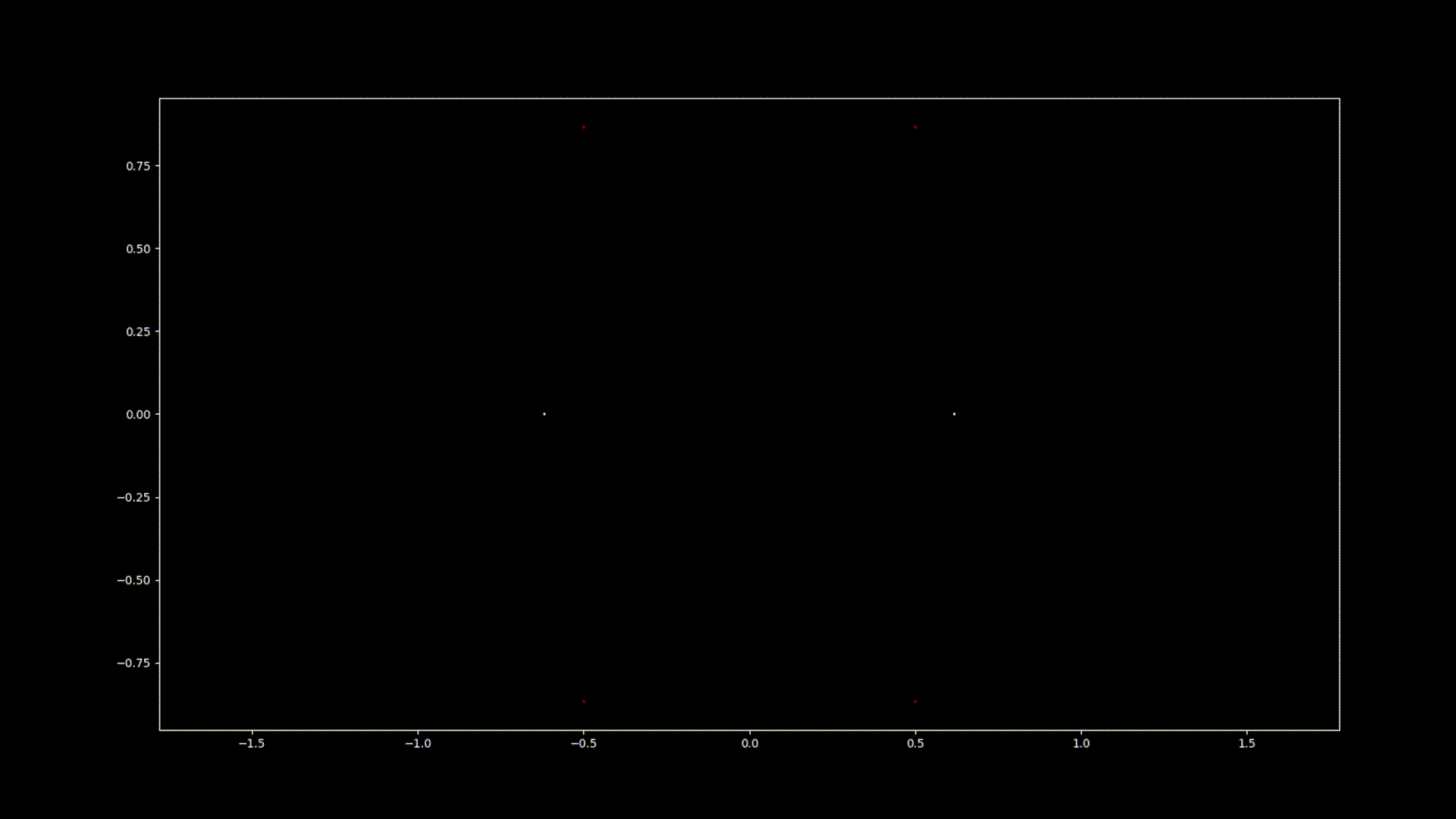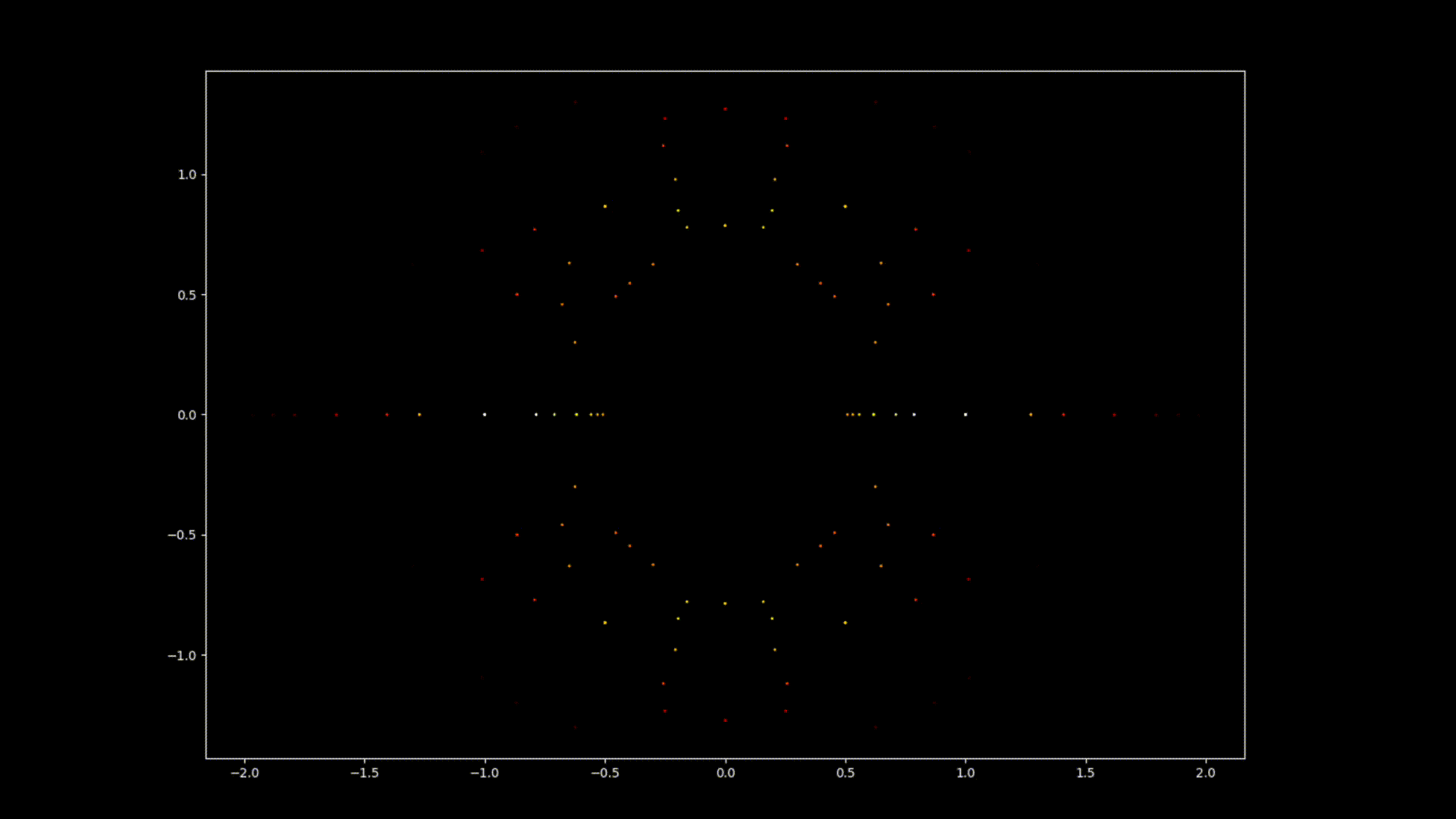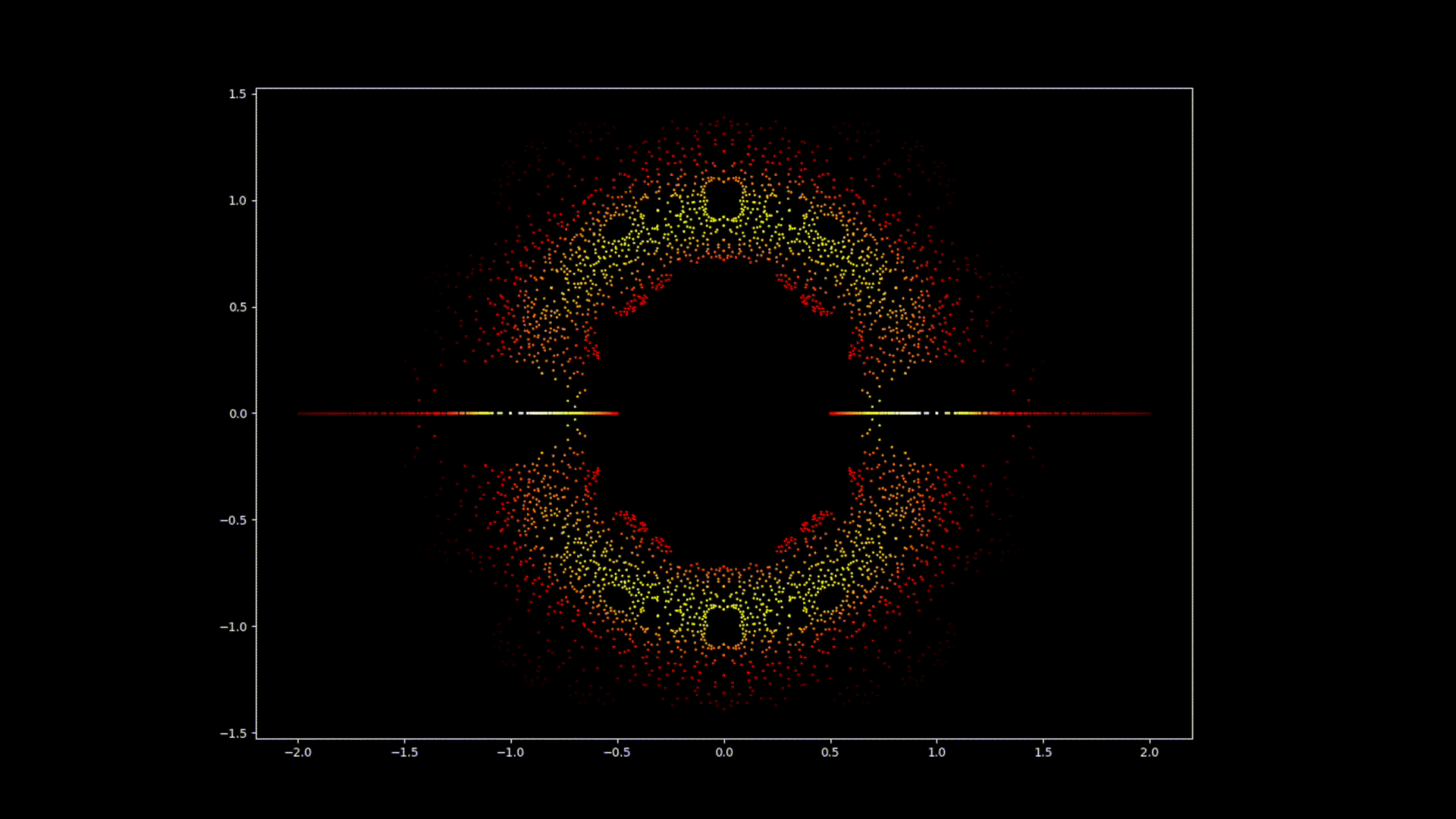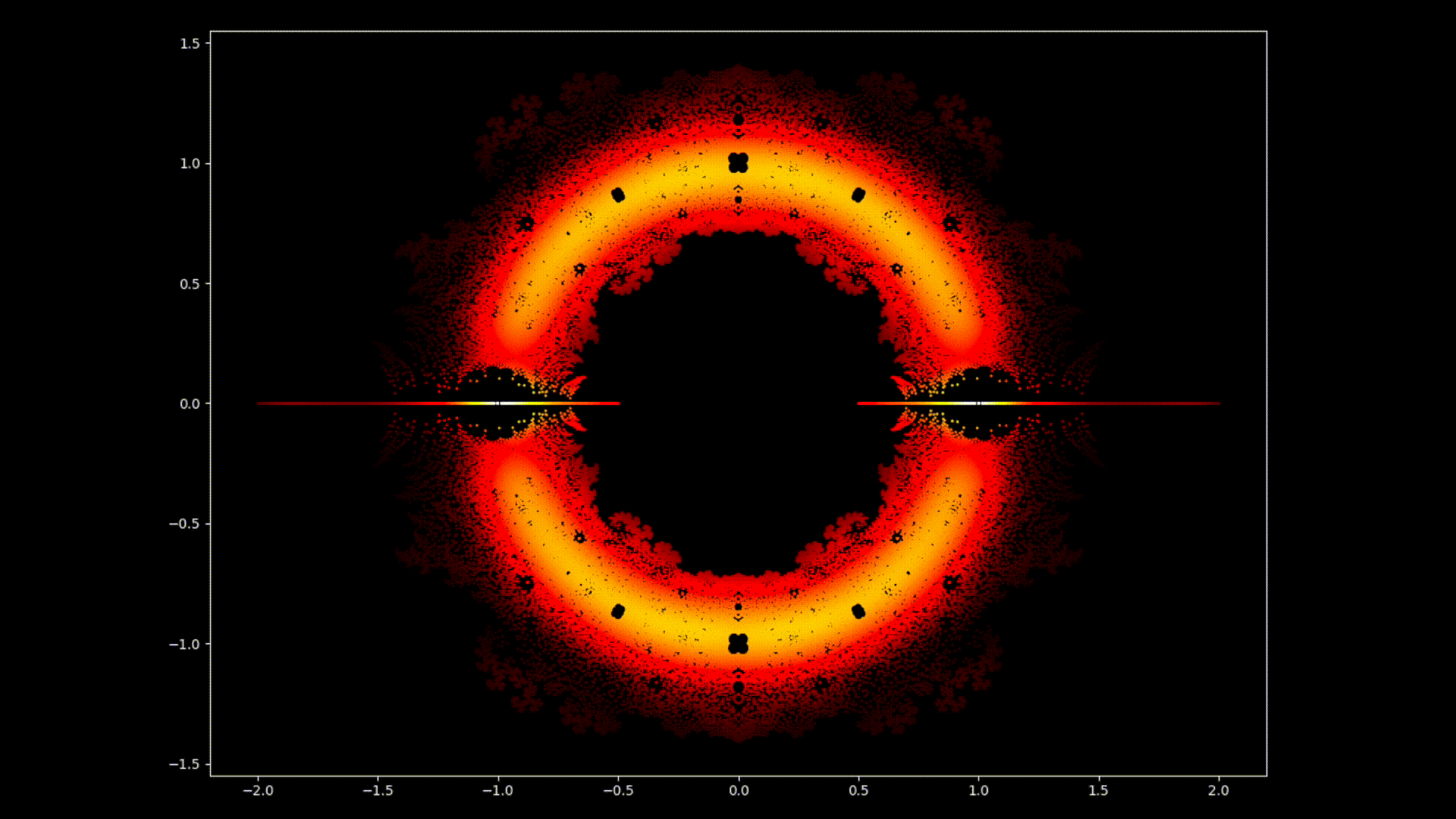
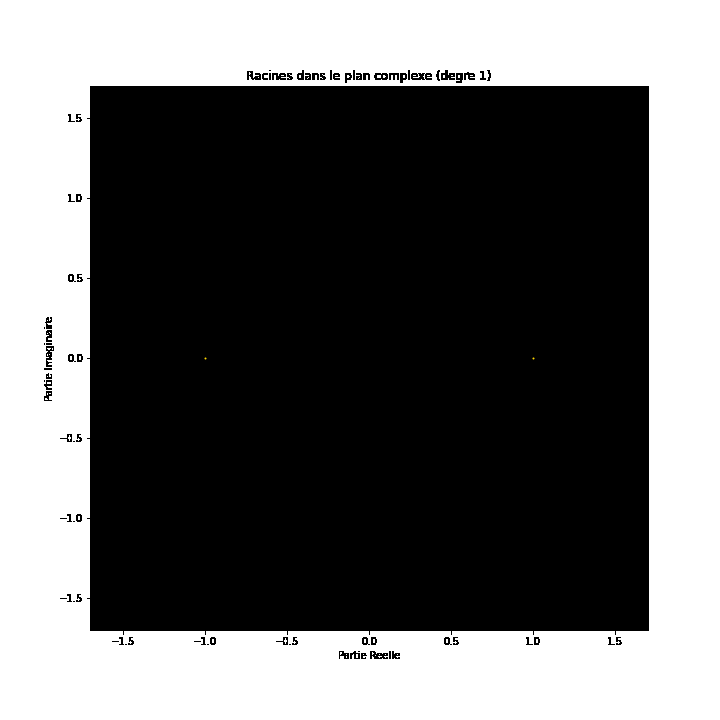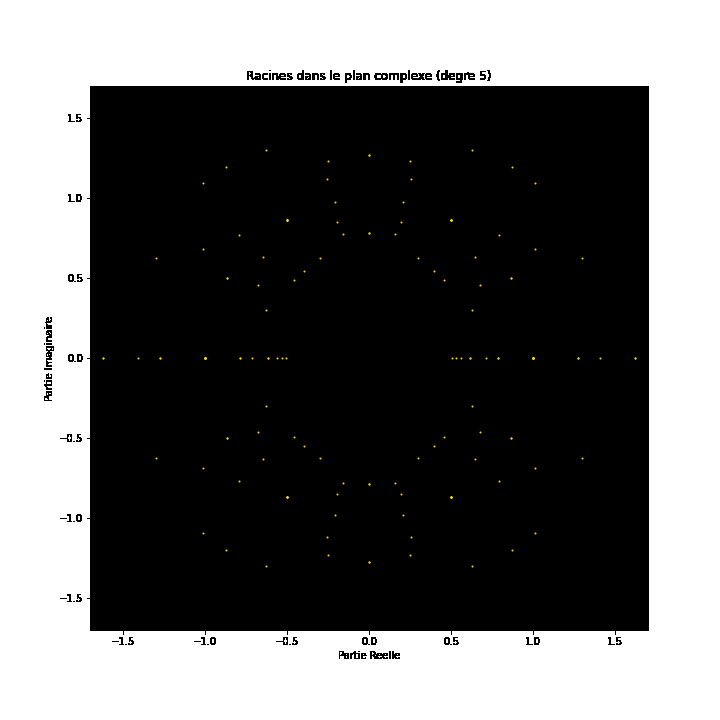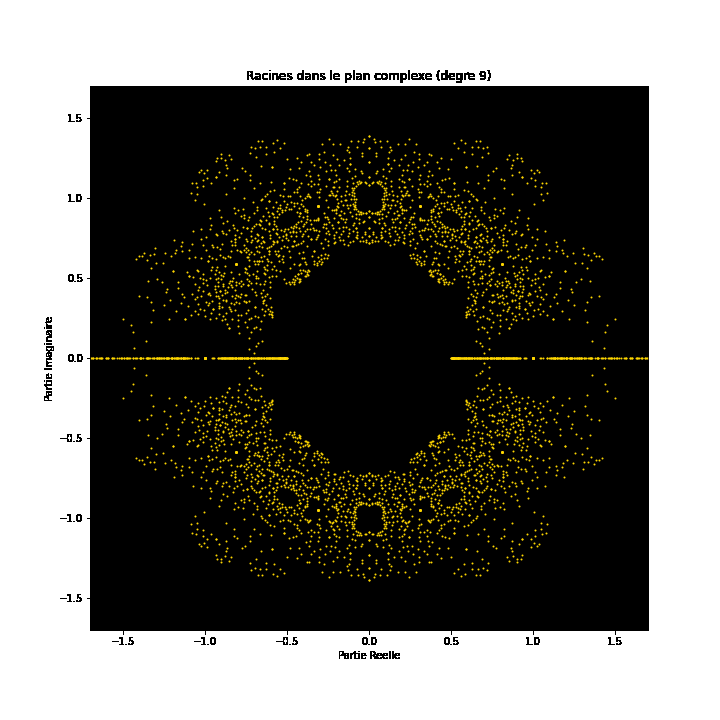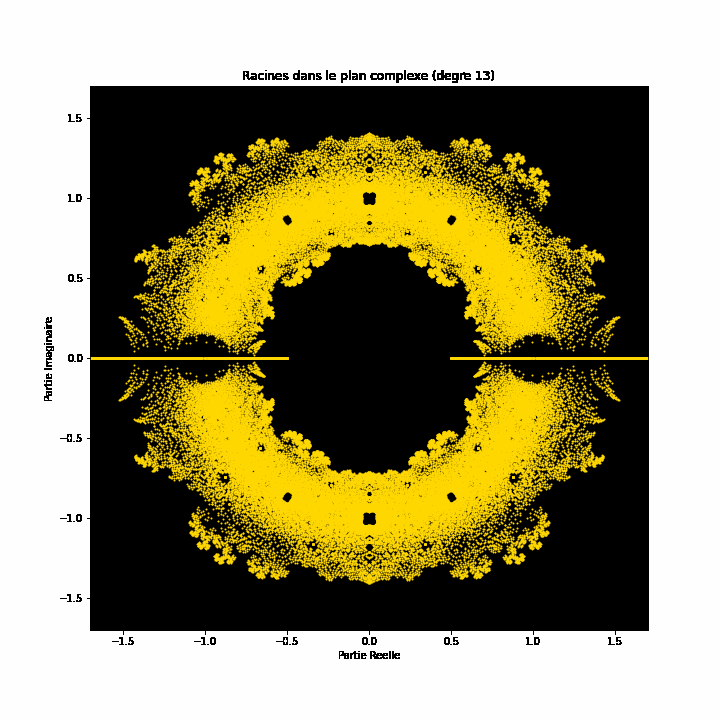
Auf den ersten Blick mögen Polynomgleichungen abstrakte Konstrukte sein, eine Abfolge von Zahlen und Variablen, die scheinbar willkürlich angeordnet sind. Doch unter dieser Oberfläche verbirgt sich eine verborgene Ordnung. Eine symmetrische Harmonie, die darauf wartet, entdeckt zu werden. Auch die Lösungen einer Gleichung, bekannt als die Wurzeln oder Nullstellen des Polynoms, haben eine tiefe Verbindung zum Konzept der Symmetrie. Diese Symmetrie kann auch auf den Bildern dieses EML-Projekts beobachtet werden, in denen wir die Wurzeln von Polynomen mit den Koeffizienten 1 und -1 sehen können. Diese werden auf der komplexen Ebene symmetrisch dargestellt, indem für jede Wurzel ein Punkt gezeichnet wird. Reelle Wurzeln erscheinen auf der horizontalen Achse und komplexe Wurzeln auf der vertikalen Achse. Wir können die einzelnen Punkte, welche eine Wurzel darstellen, nicht sehen da es zu viele gibt. Tatsächlich gibt es 805.306.368 Wurzeln für ein Polynom vom Grad 24, die zusammen eine bizarre Feuerkugel bilden. Diese visuellen Darstellungen liefern Einblicke in die Verteilung, Symmetrie und das Verhalten der Polynomwurzeln, die uns helfen, ihre Eigenschaften und Beziehungen zu verstehen. Sie zeigen auch, wie schön Mathematik sein kann.

Kredite: Diese Bilder wurden im Rahmen des Experimental Mathematics Lab-Projekts mit dem Titel ''Visualising Roots of algebraic Numbers'' erstellt, an dem viele Studenten beteiligt waren, nämlich Claudia Marichal, Catia Alves Piro, Salma Belmir, Mikala Eisen, Melissa Genoud, Lynn Hellenbrand, Tom Kasel, Christophe Thelen, Gil Moes und Mirza Muharemovic, und wurde von Prof. Gabor Wiese, Dr. Guendalina Palmirotta und Dr. Thierry Meyrath betreut.

FWeitere Informationen: Besuchen Sie die Webseite von John Baez "The beauty of roots" und unsere Experimental Mathematics Lab Webseite.

Andere Sprachen: