Bizarre fireballs

fr

  La symétrie est synonyme d'équilibre et d'harmonie, et elle est partout autour de nous. Pensez aux ailes d'un papillon, parfaitement équilibrées de chaque côté, comme une image miroir. Les fleurs ont des pétales symétriques, chacune reflétant les autres autour de lui. Et si vous levez les yeux vers les étoiles, vous verrez des galaxies tourner de manière symétrique. Il y a de la symétrie partout : dans l'art, dans la nature, et même à l'intérieur de nos corps ! Avez-vous déjà vu un bâtiment avec des fenêtres parfaitement assorties de chaque côté ? C'est la symétrie à l'oeuvre. Les artistes aiment aussi la symétrie. Ils l'utilisent pour créer de beaux motifs et des designs. Même les enfants sont confrontés à l'art symétrique dès leur plus jeune âge lorsqu'ils dessinent un mandala ou un papillon. Et dans les peintures, les artistes utilisent la symétrie pour donner à leurs compositions une sensation d'ordre et d'équilibre. Mais la symétrie n'est pas réservée à l'art, elle est aussi présente dans la science. Les scientifiques utilisent la symétrie pour comprendre le monde qui nous entoure. Ils utilisent les mathématiques pour décrire comment les choses se déplacent et changent, et la symétrie les aide à voir des motifs et des connexions.

Animation hot roots Animation roots Animation zoom roots


Mais qu'est-ce que la symétrie exactement ?
La symétrie incarne l'idée que certaines transformations, telles que la réflexion (comme mettre un miroir au milieu d'un papillon), la rotation (comme tourner l'image d'un soleil) ou la translation (présente dans un rayon de miel), laissent un objet inchangé ou invariant, révélant des motifs et des relations fondamentales.

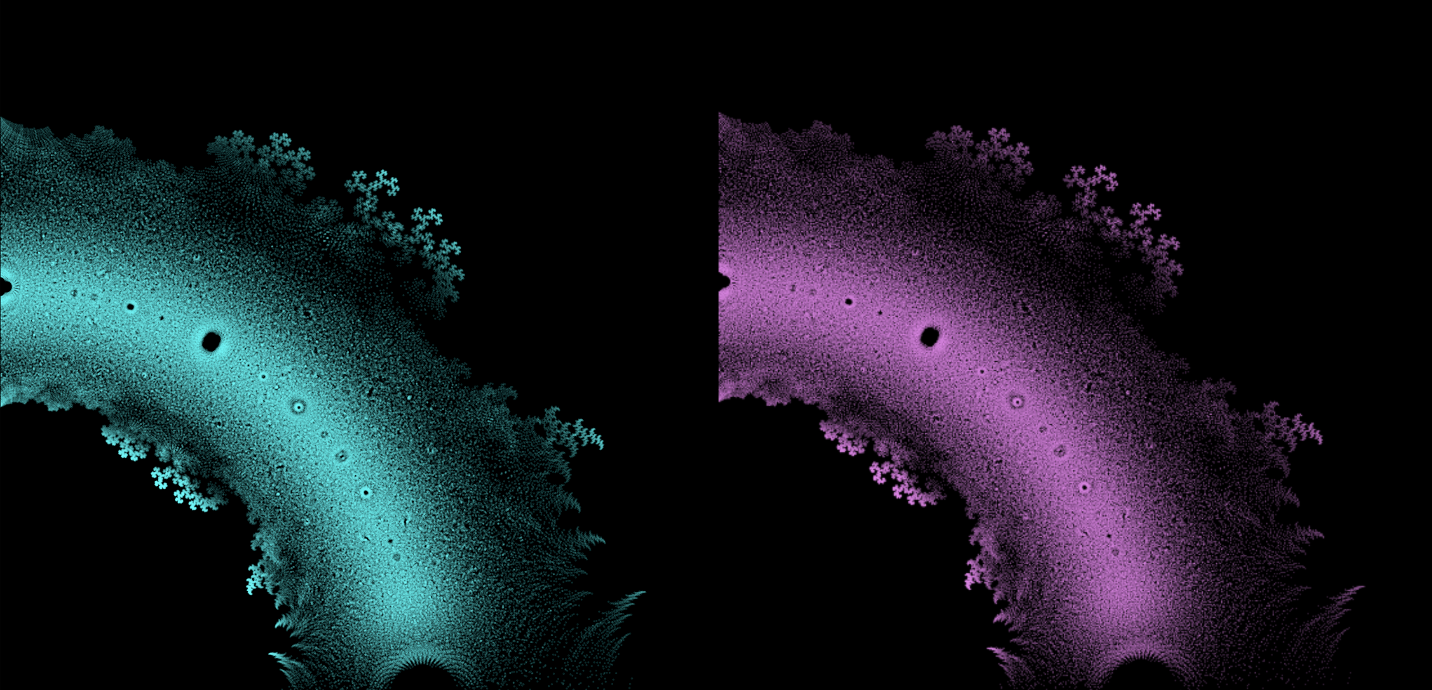
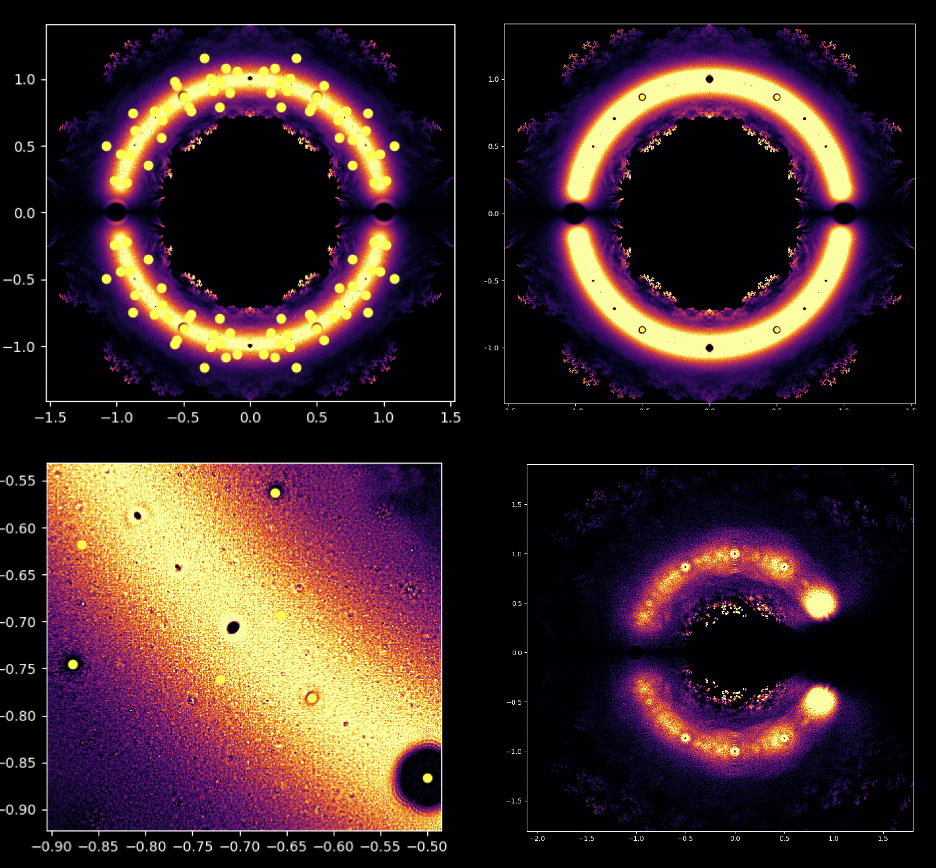
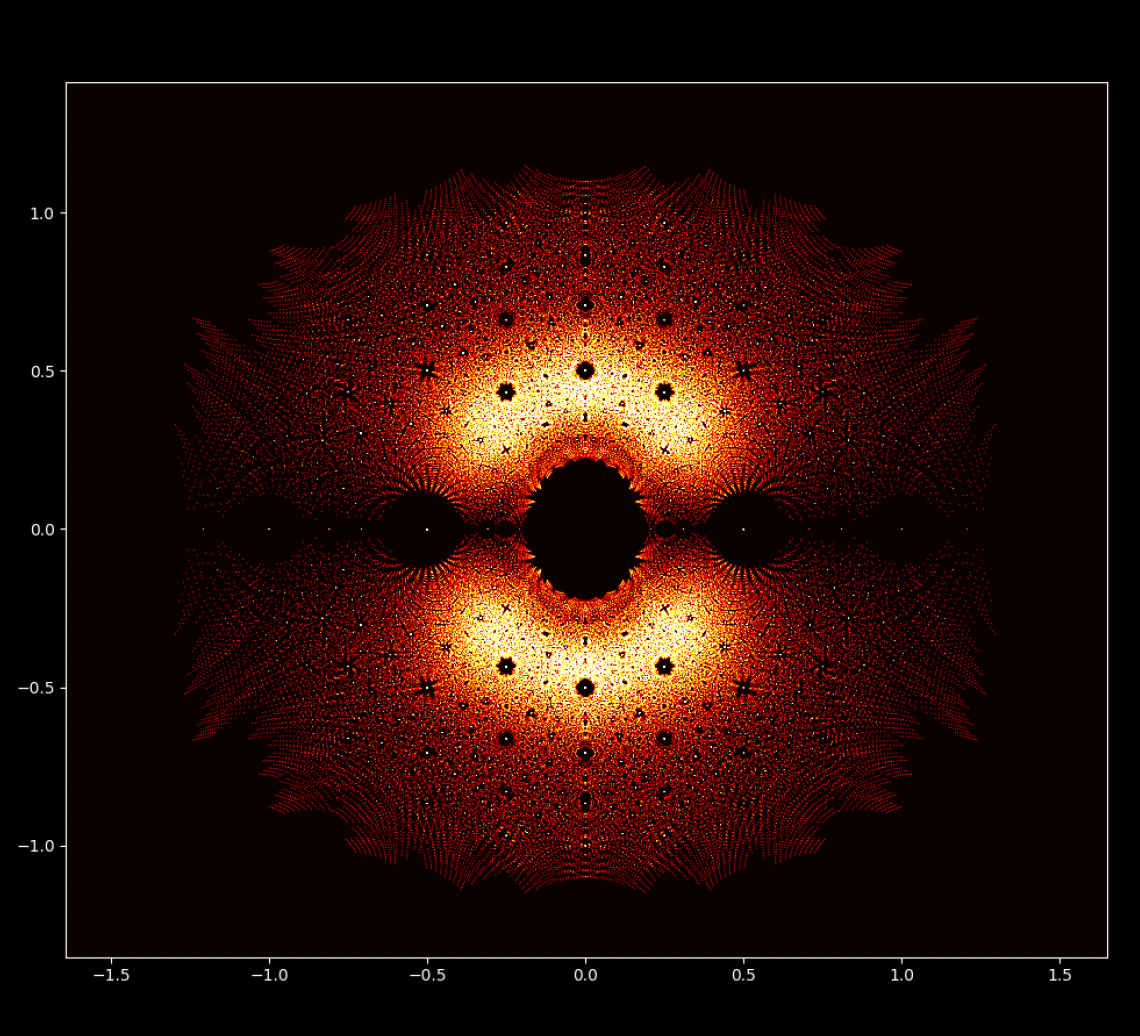
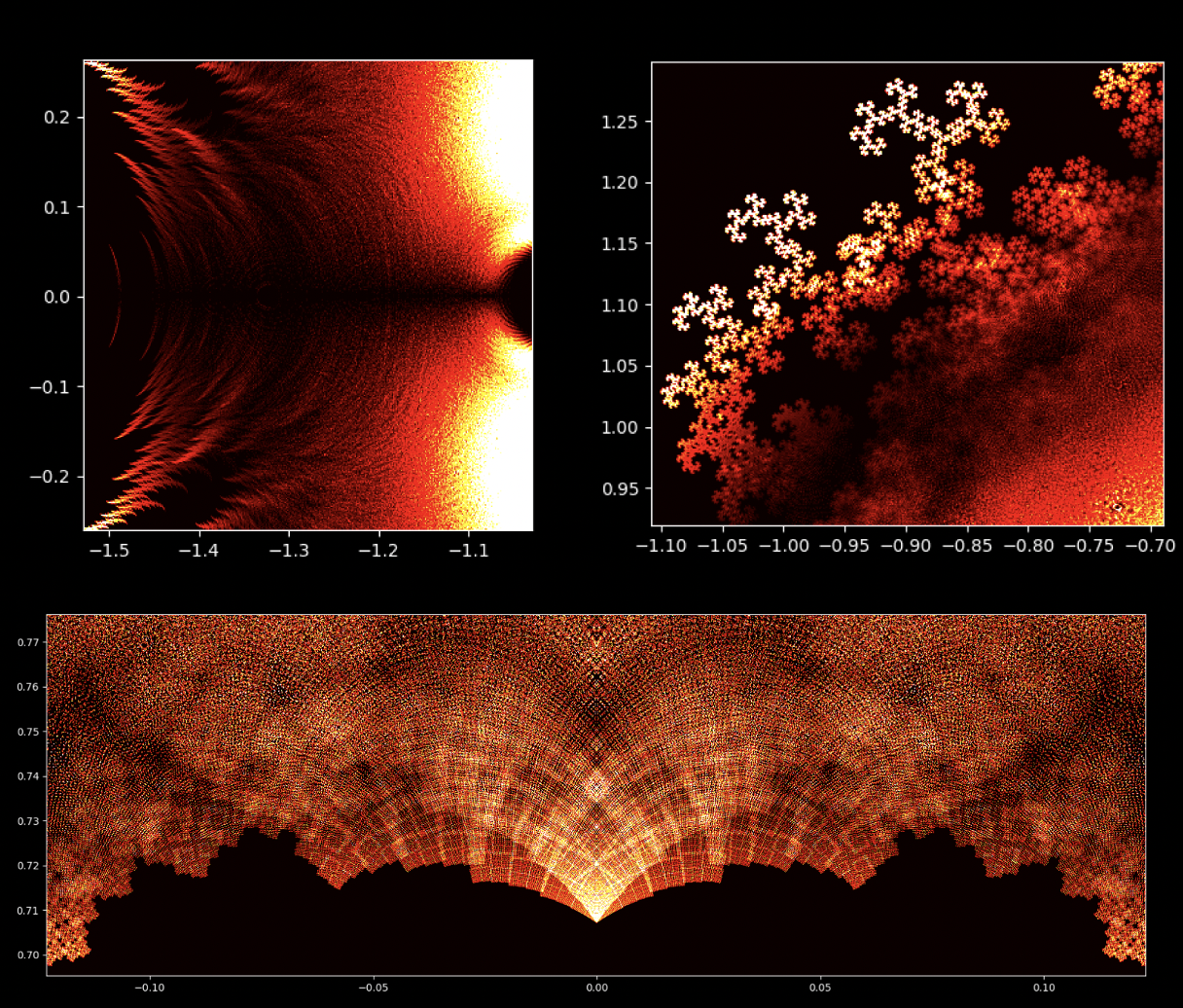
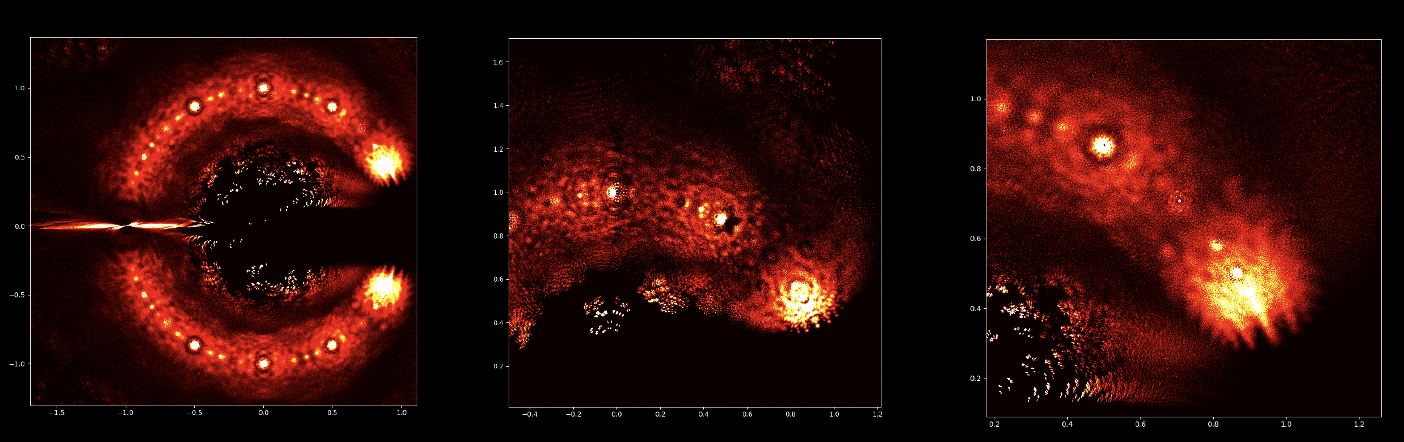
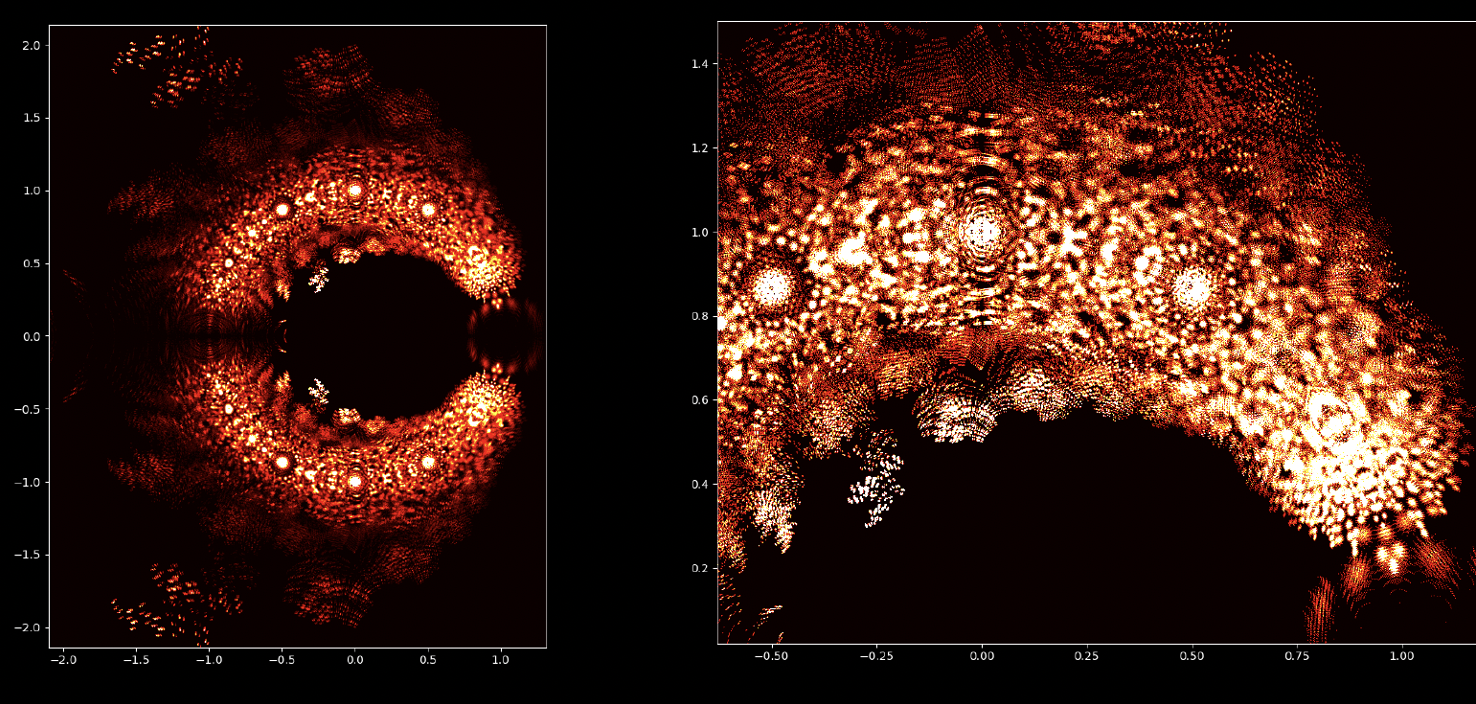
Coloured roots Zoom on the roots Flash roots Fireworks roots Fractals Fire roots Roots that look like worms


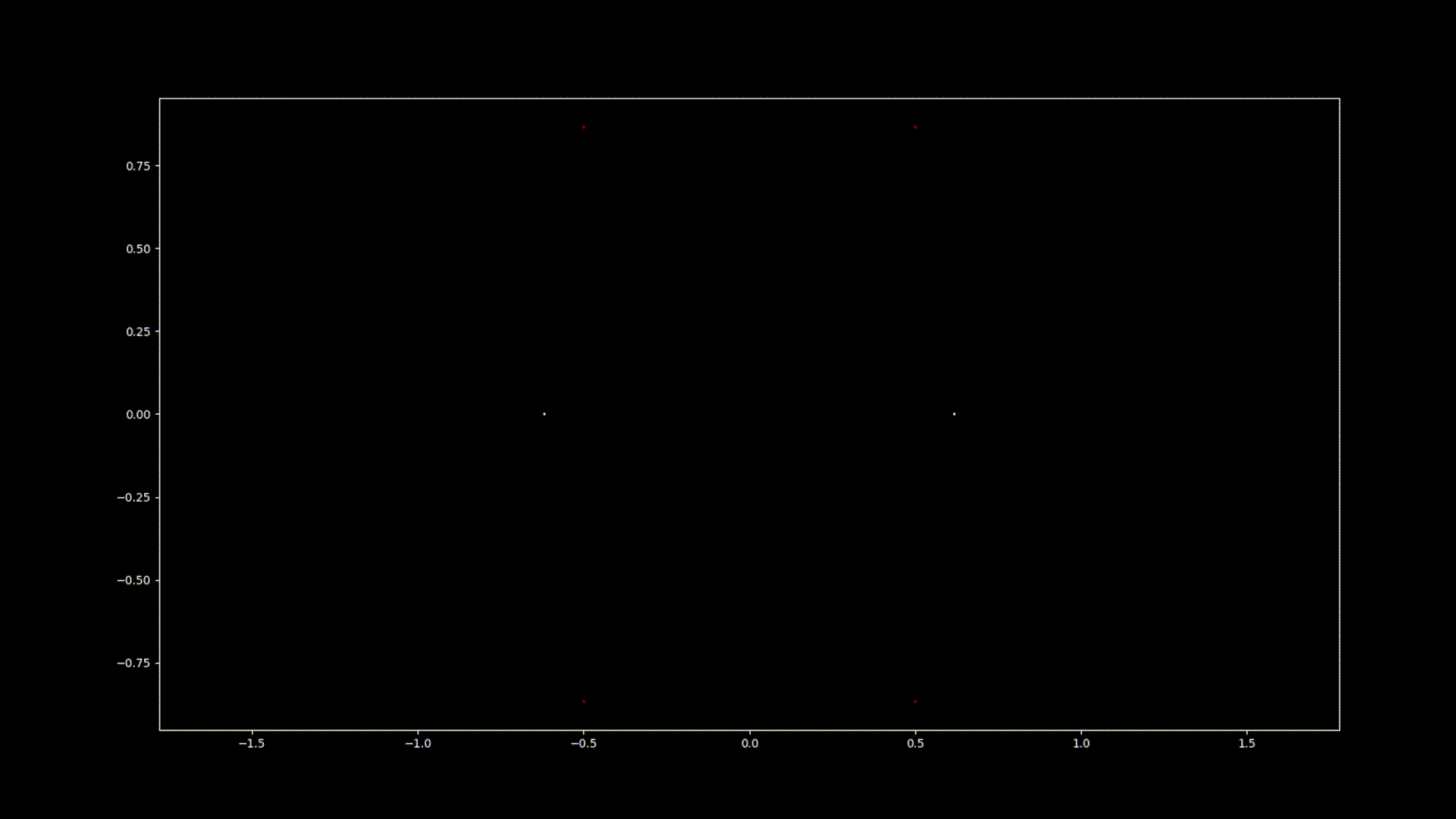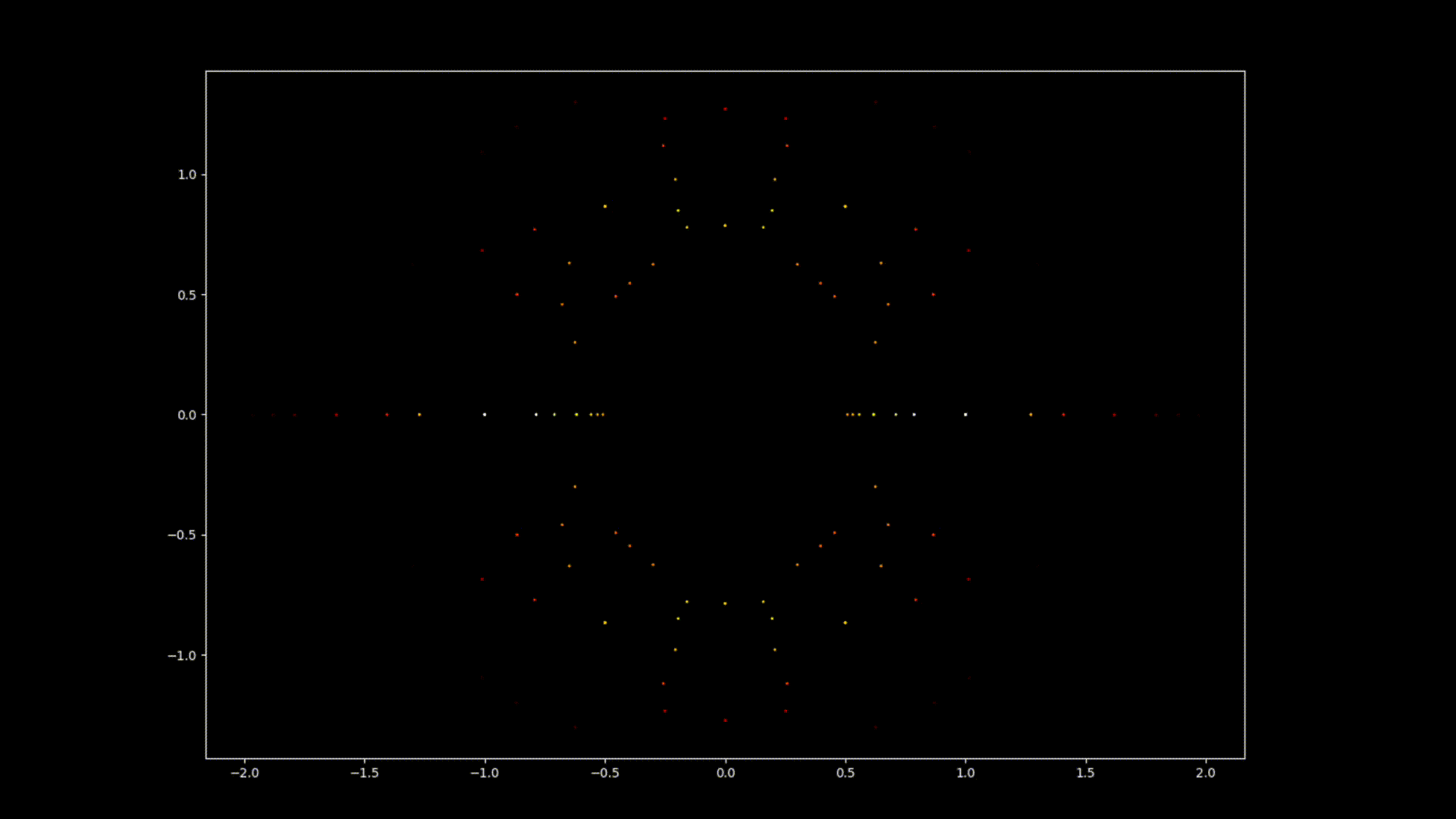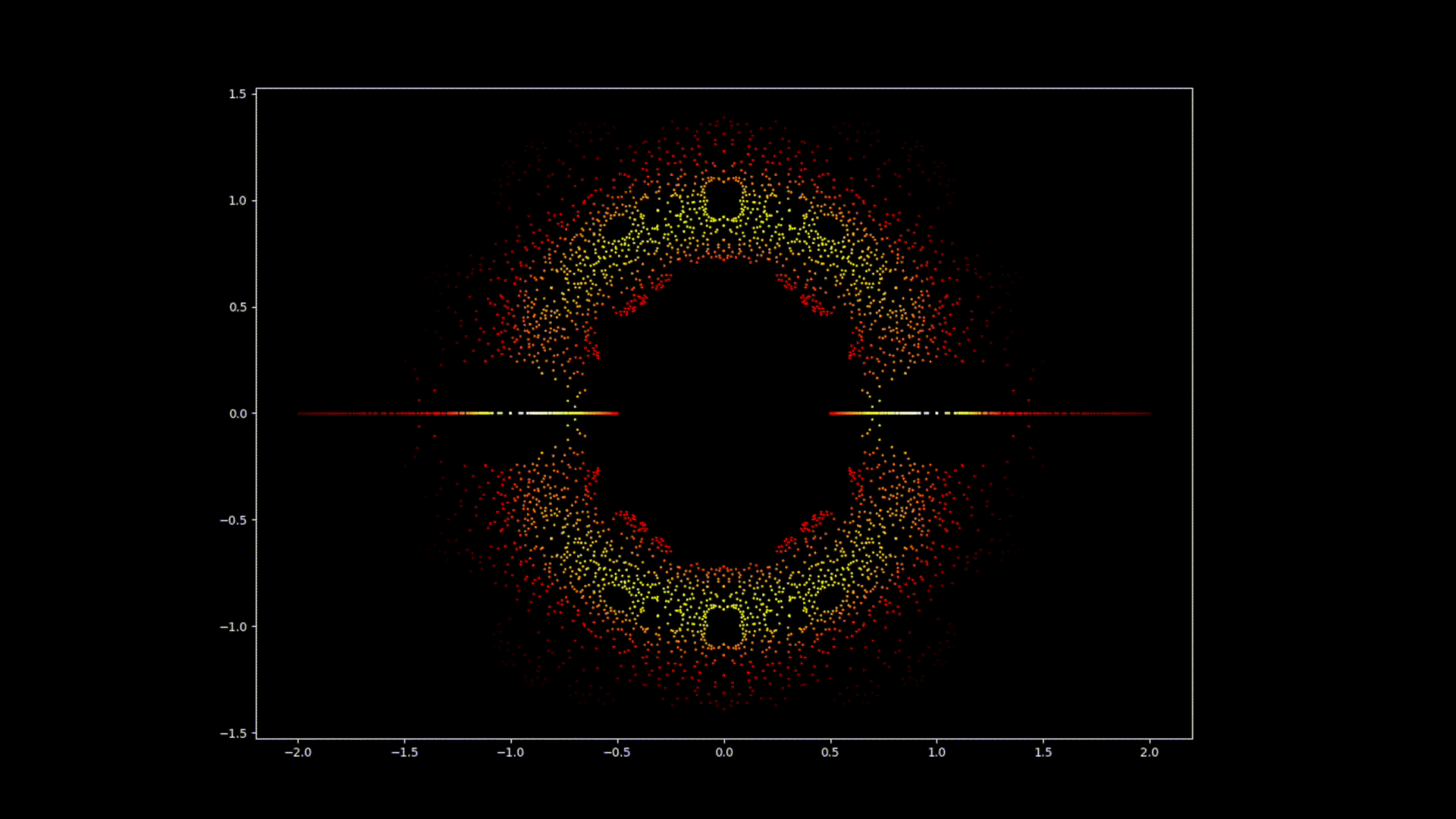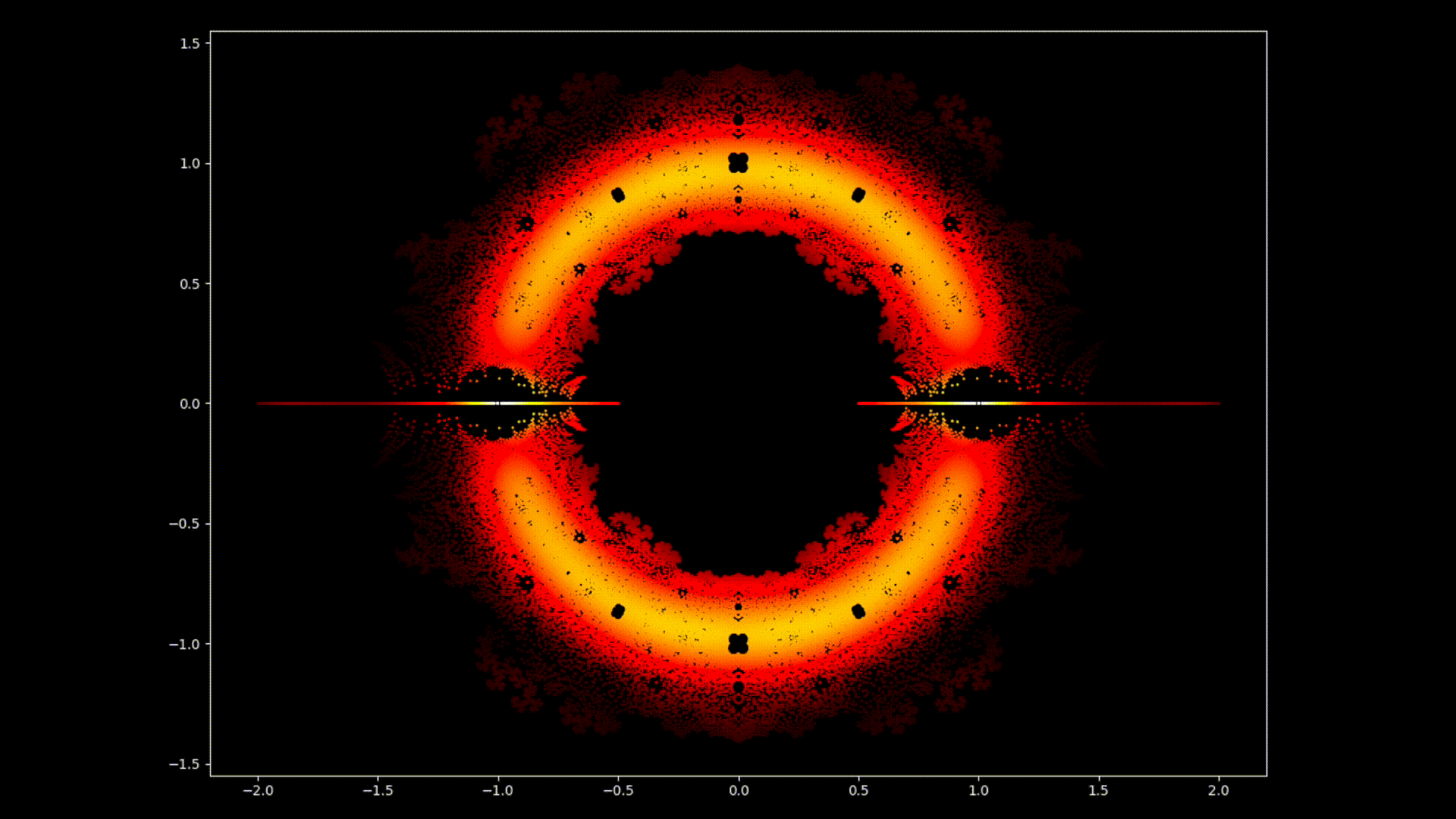
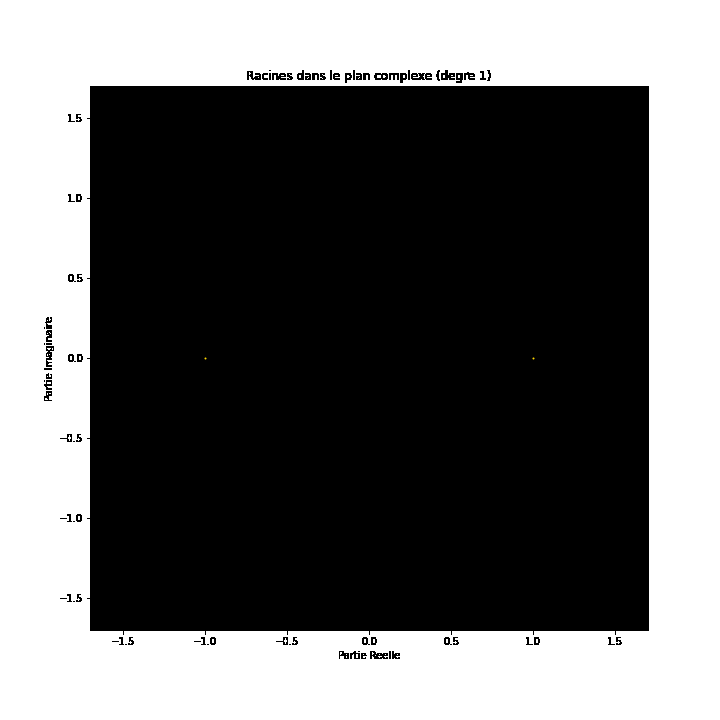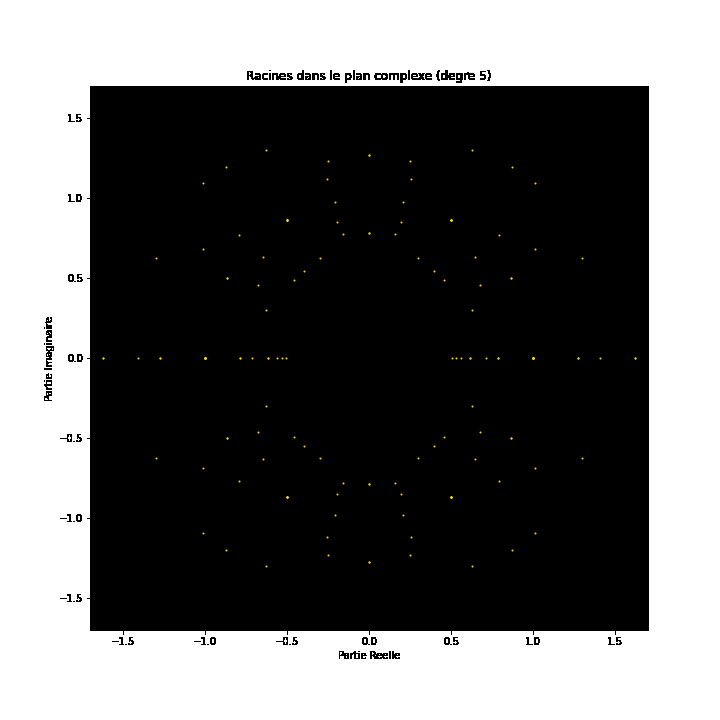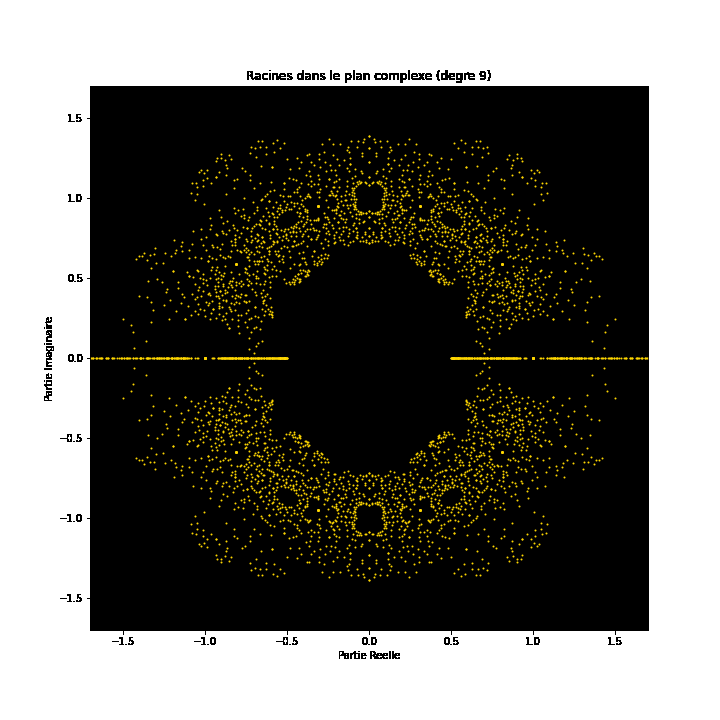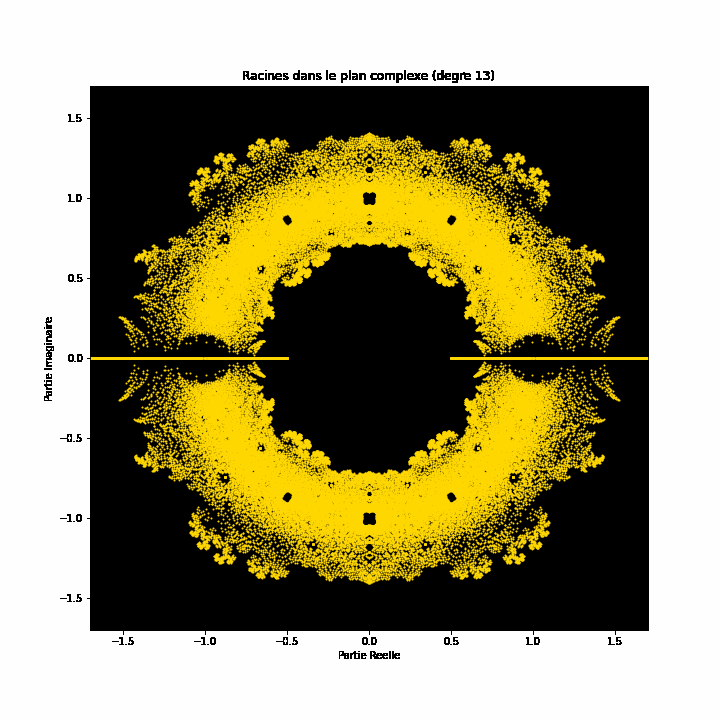
À première vue, les équations polynomiales peuvent sembler être des constructions abstraites, des ensembles de nombres et de variables disposés de manière arbitraire. Cependant, sous cette surface se cache un ordre caché, une harmonie symétrique qui attend d'être découverte. Les solutions d'une équation, connues sous le nom de racines ou zéros du polynôme, ont une connexion profonde avec le concept de symétrie. Cette symétrie peut également être observée dans les images de ce projet EML, sur lesquelles nous pouvons observer les racines des polynômes avec des coefficients 1 et -1, qui sont visualisés sur le plan complexe de manière symétrique, en traçant un point pour chaque racine. Les racines réelles apparaissent sur l'axe horizontal et les racines complexes sur l'axe vertical. Nous ne pouvons pas voir les points individuels tracés pour chaque racine car il y en a trop. En fait, il y a 805 306 368 racines pour un polynôme de degré 24, qui forment toutes ensemble, une boule de feu bizarre. Ces représentations visuelles fournissent des informations sur la distribution, la symétrie et le comportement des racines polynomiales, nous aident à comprendre leurs propriétés et leurs relations, mais elles montrent aussi à quel point les mathématiques peuvent être belles.

Crédits: Ces images ont été créées dans le cadre du projet du experimental Mathematics Lab intitulé « Visualisation des racines des nombres algébriques », auquel ont participé de nombreux étudiants, à savoir Claudia Marichal, Catia Alves Piro, Salma Belmir, Mikala Eisen, Melissa Genoud, Lynn Hellenbrand, Tom Kasel, Christophe Thelen, Gil Moes et Mirza Muharemovic, et a été supervisé par Prof. Gabor Wiese, Dr. Guendalina Palmirotta et Dr. Thierry Meyrath.

Plus d'informations: Consultez le site web de John Baez "The beauty of roots" et notre site web Experimental Mathematics Lab.

Autres langues: