Bizarre fireballs

lux

  Symmetrie ass alles ëm d’Gläichgewiicht an Harmonie, an et ass iwwerall ronderëm eis. Denkt un d'Flilleke vun engem Päiperlek, si sinn op béide Säite perfekt ausgeglach, wéi e Spigelbild. Blummen hu symmetresch Bléieblieder, an all eenzelt Blat spigelt déi aner ronderëm. Wann Dir op d'Stäre kuckt, da gesitt Dir Galaxien déi op eng symmetresch Manéier dréinen. Et gëtt Symmetrie iwwerall: an der Konscht, an der Natur, an och an eisem Kierper! Hutt Dir schonns e Gebai gesi mat perfekt passende Fënsteren op all Säit? Dat ass Symmetrie op der Aarbecht. Kënschtler hunn d'Symmetrie och gär. Si benotzen et fir schéi Musteren an Designen ze kreéieren. Och Kanner gi vu jonkem Alter mat symmetrescher Konscht konfrontéiert wann se e Mandala oder e Päiperlek molen. Kënschtler benotze Symmetrie fir datt hir Kompositiounen sech equilibréiert ufillen. Awer d’Symmetrie existéiert net nëmme an der Konscht, se ass och an de Wëssenschaften ze fannen. Wëssenschaftler benotze Symmetrie fir d'Welt ronderëm eis ze verstoen. Si beschreiwe mathematesch wéi d'Saachen sech beweegen an änneren, a Symmetrie hëlleft hinne Musteren a Verbindungen ze fannen.

Animation hot roots Animation roots Animation zoom roots


Awer wat genee ass Symmetrie?
Symmetrie verkierpert d'Iddi datt verschidden Transformatiounen, wéi Reflexioun (déi ass ze fanne wann Dir e Spigel op de Kierper vun engem Päiperlek setzt), Rotatioun (wann dir d'Bild vun enger Sonn dréien) oder parallel Verschibung (wat an enger Hunnegwab ze gesinn ass), en Objet onverännert hannerloossen a fundamental Musteren a Relatiounen opzeweisen.

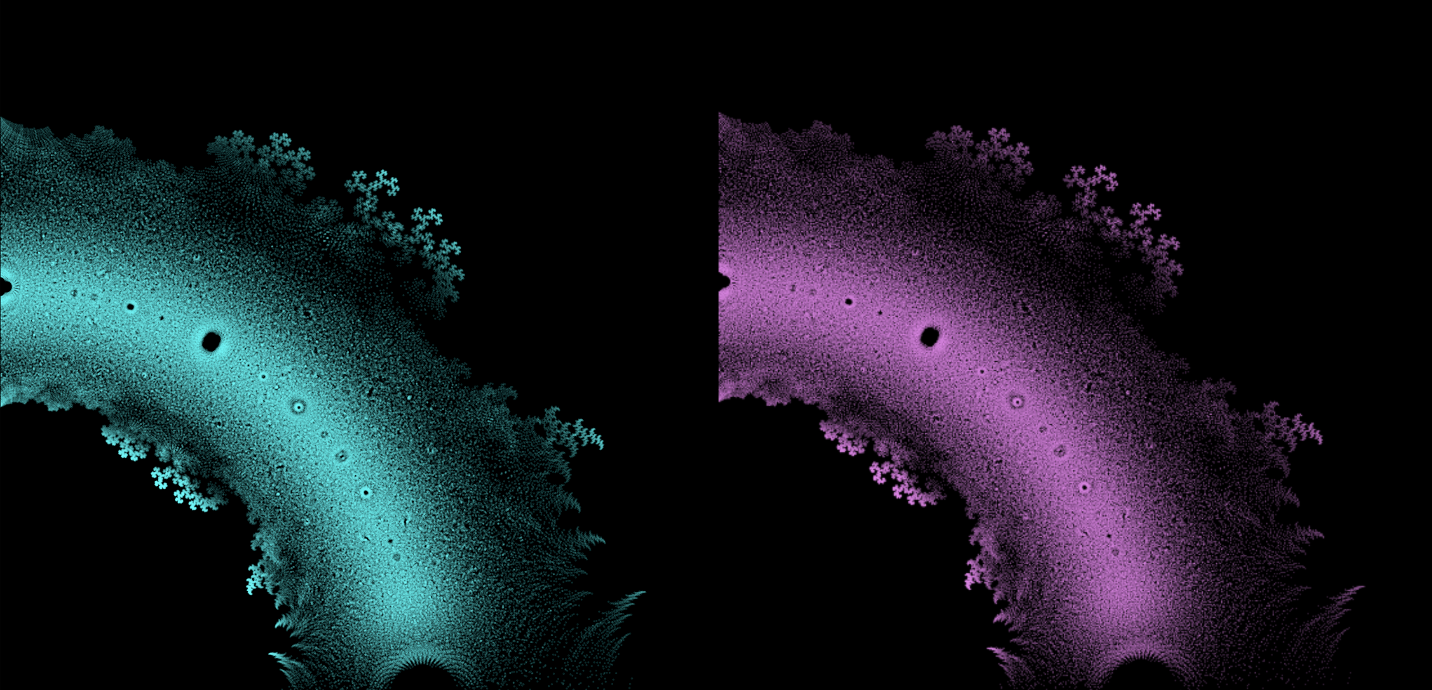
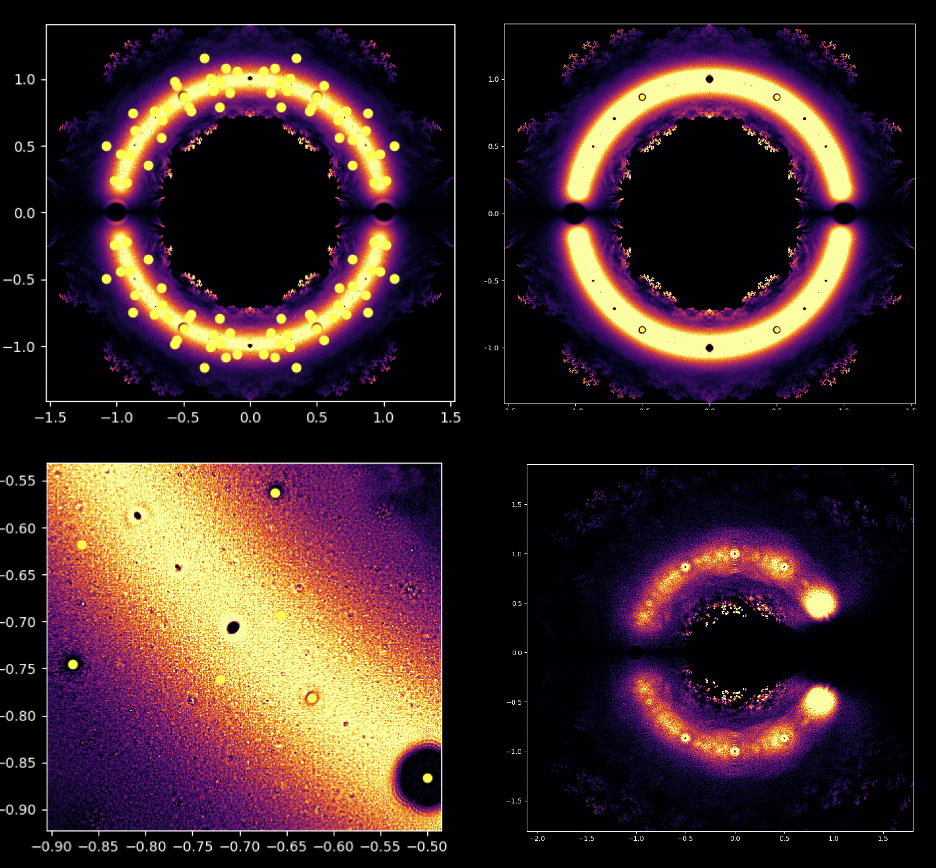
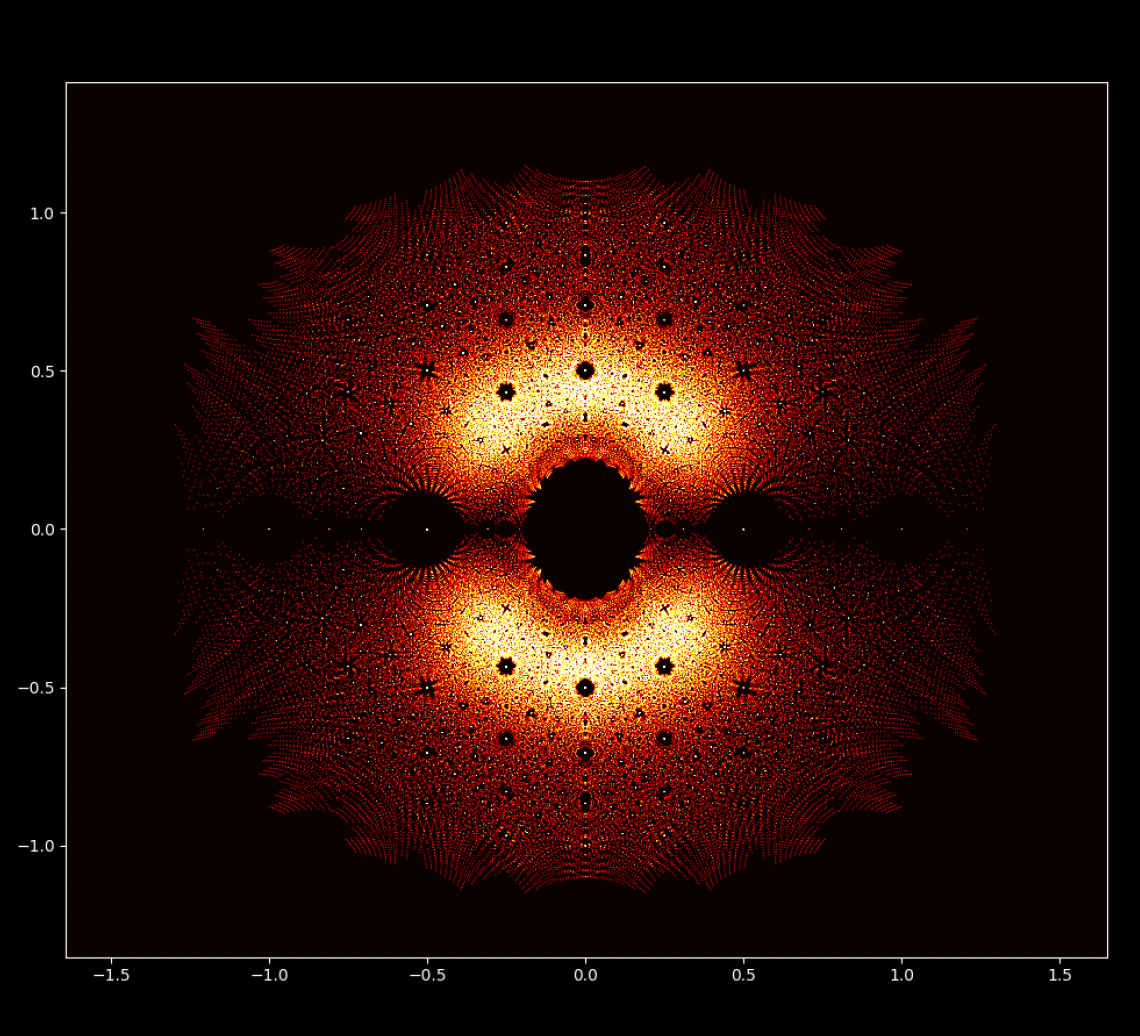
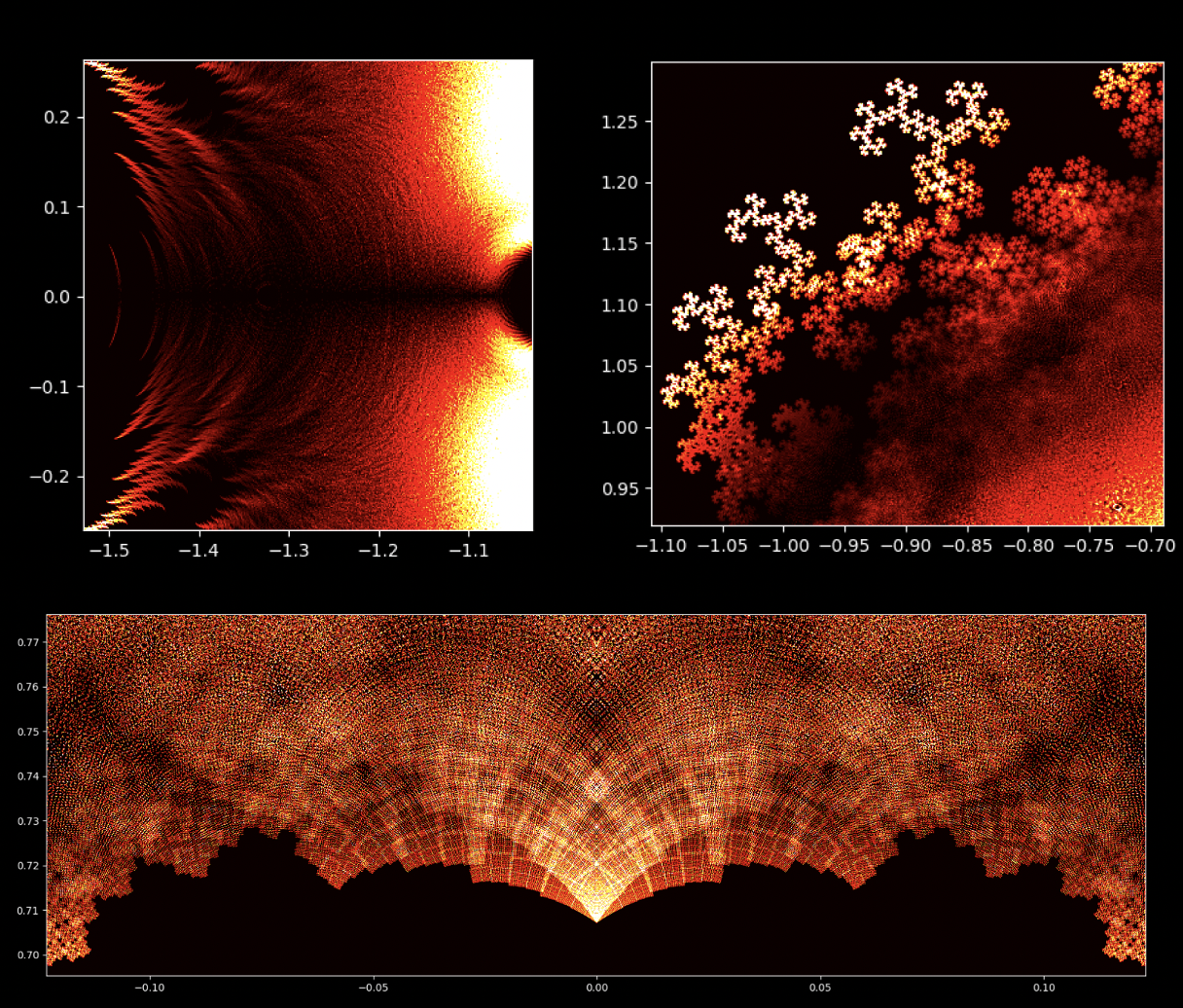
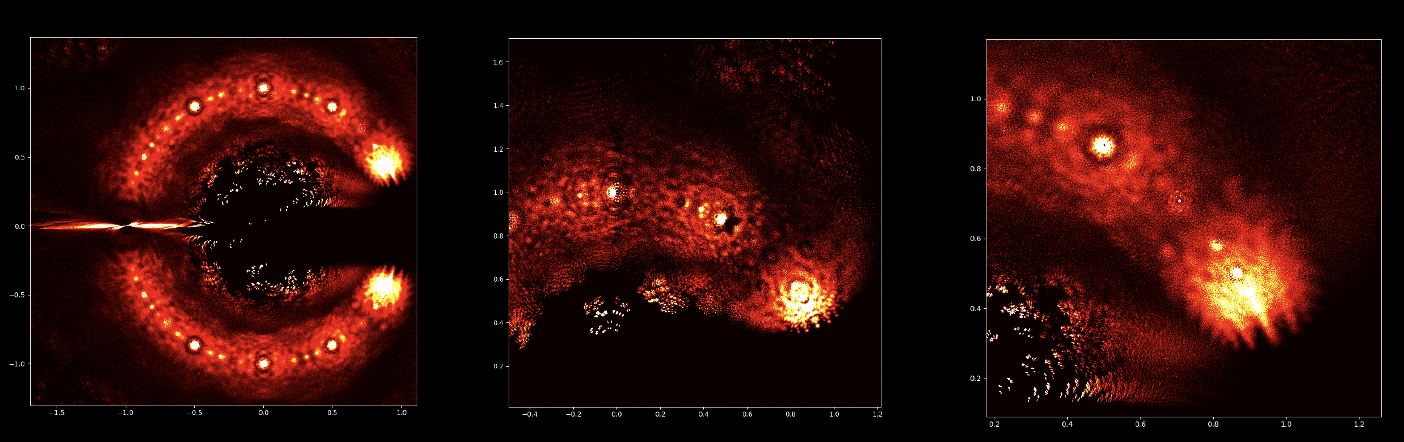
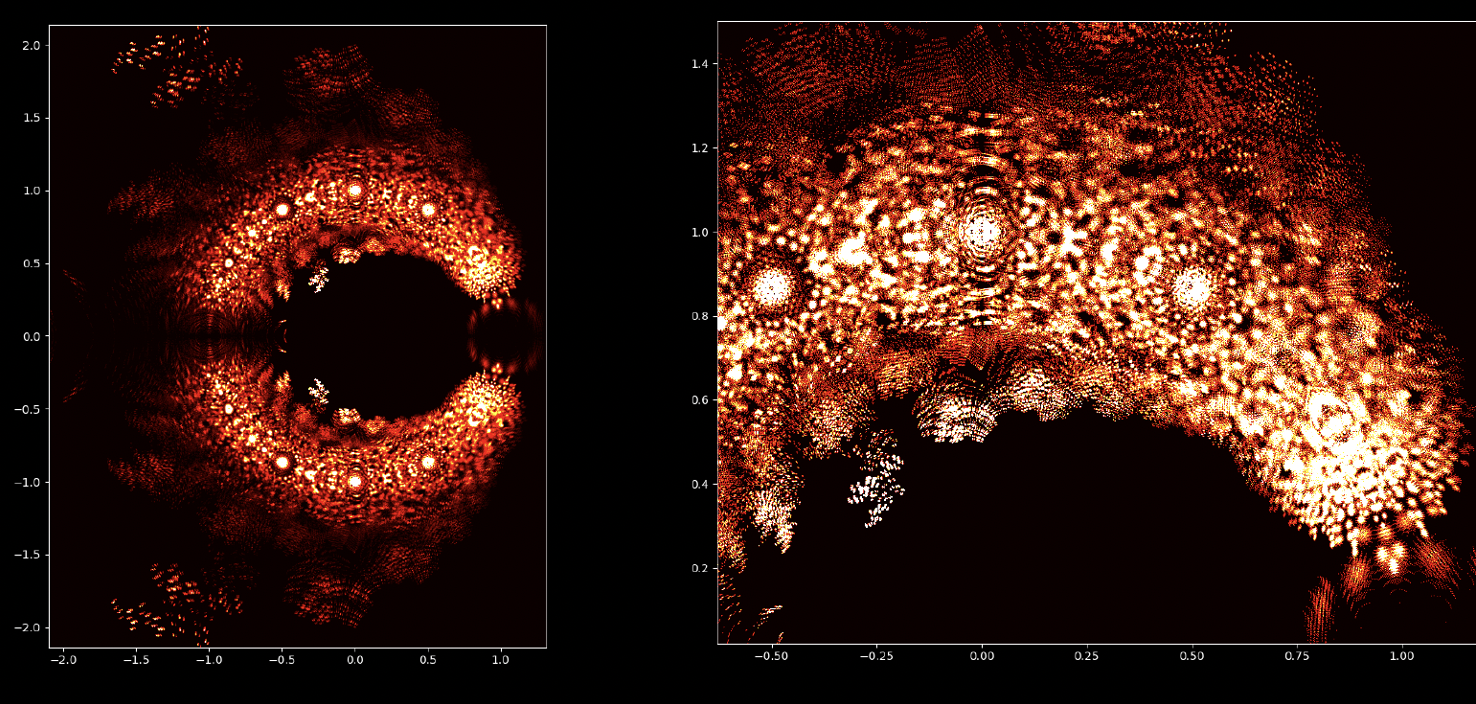
Coloured roots Zoom on the roots Flash roots Fireworks roots Fractals Fire roots Roots that look like worms


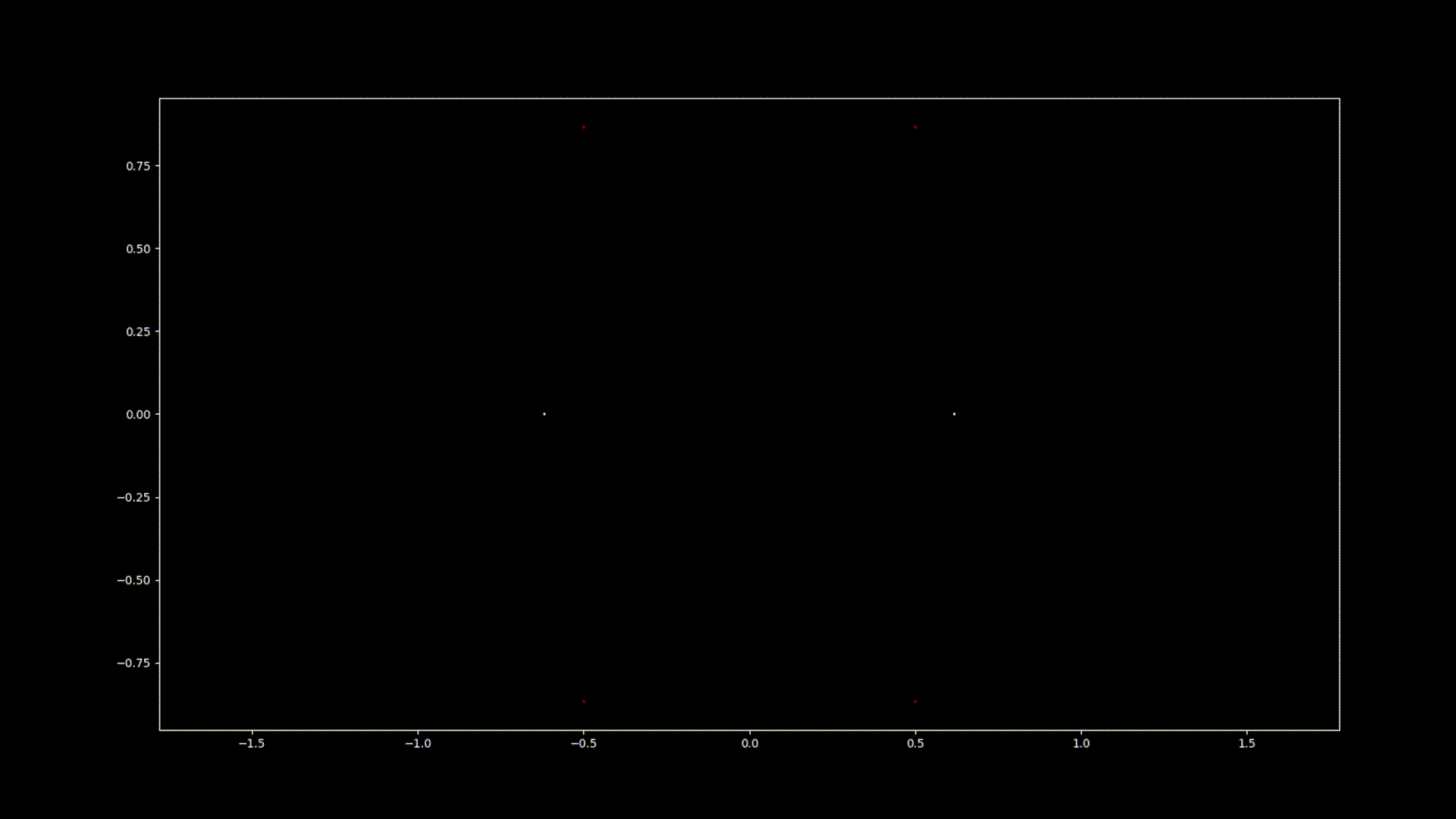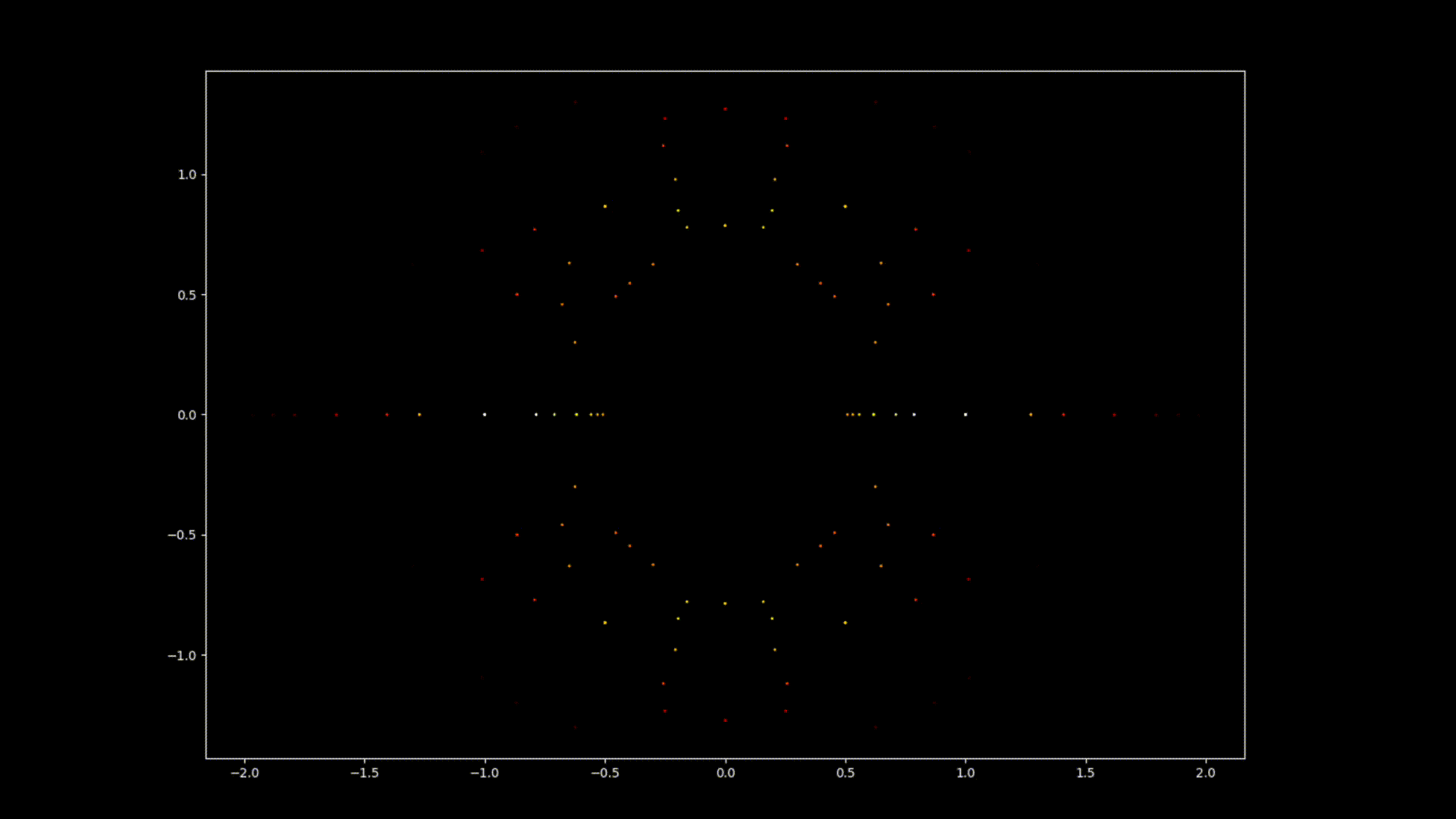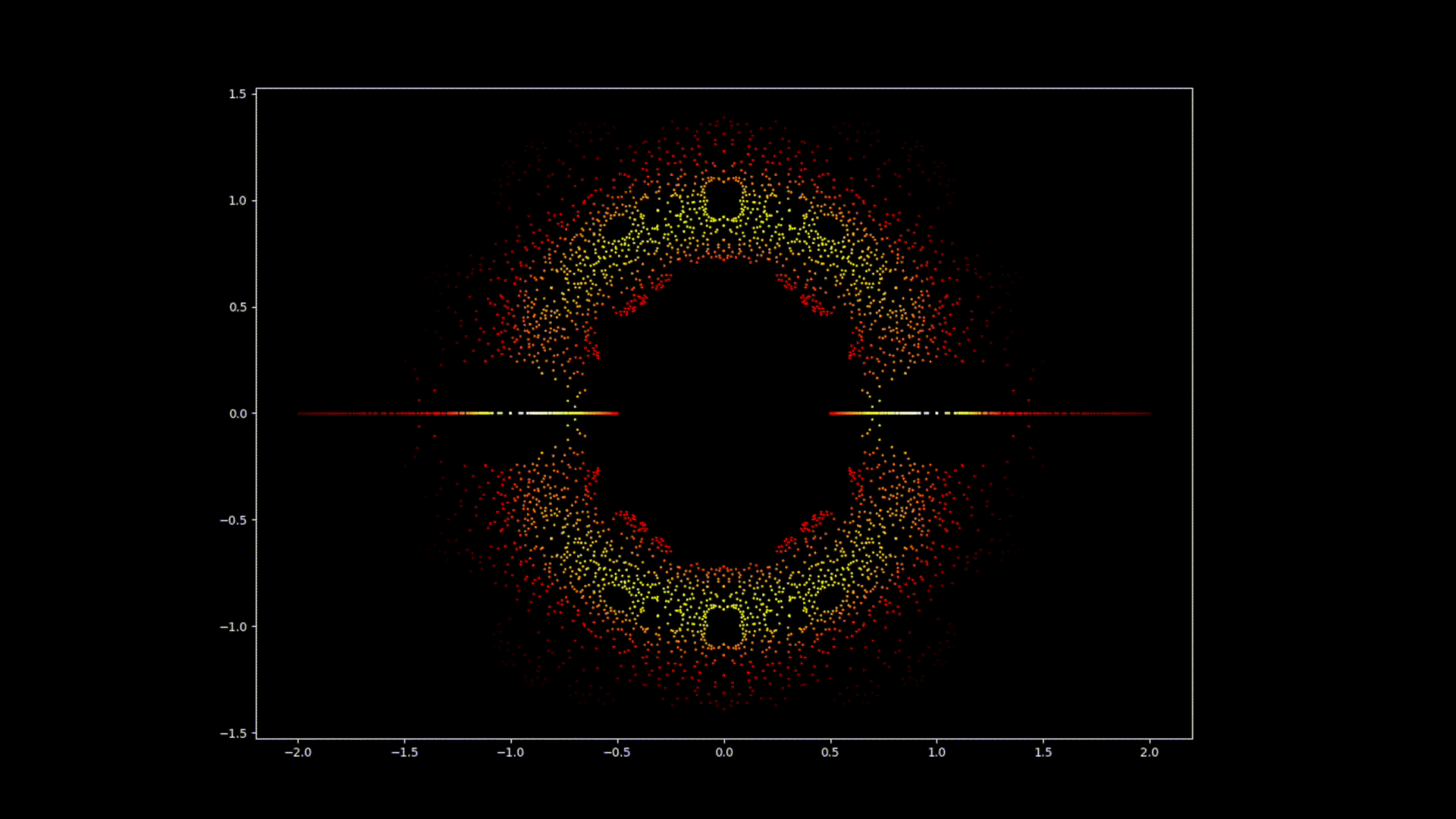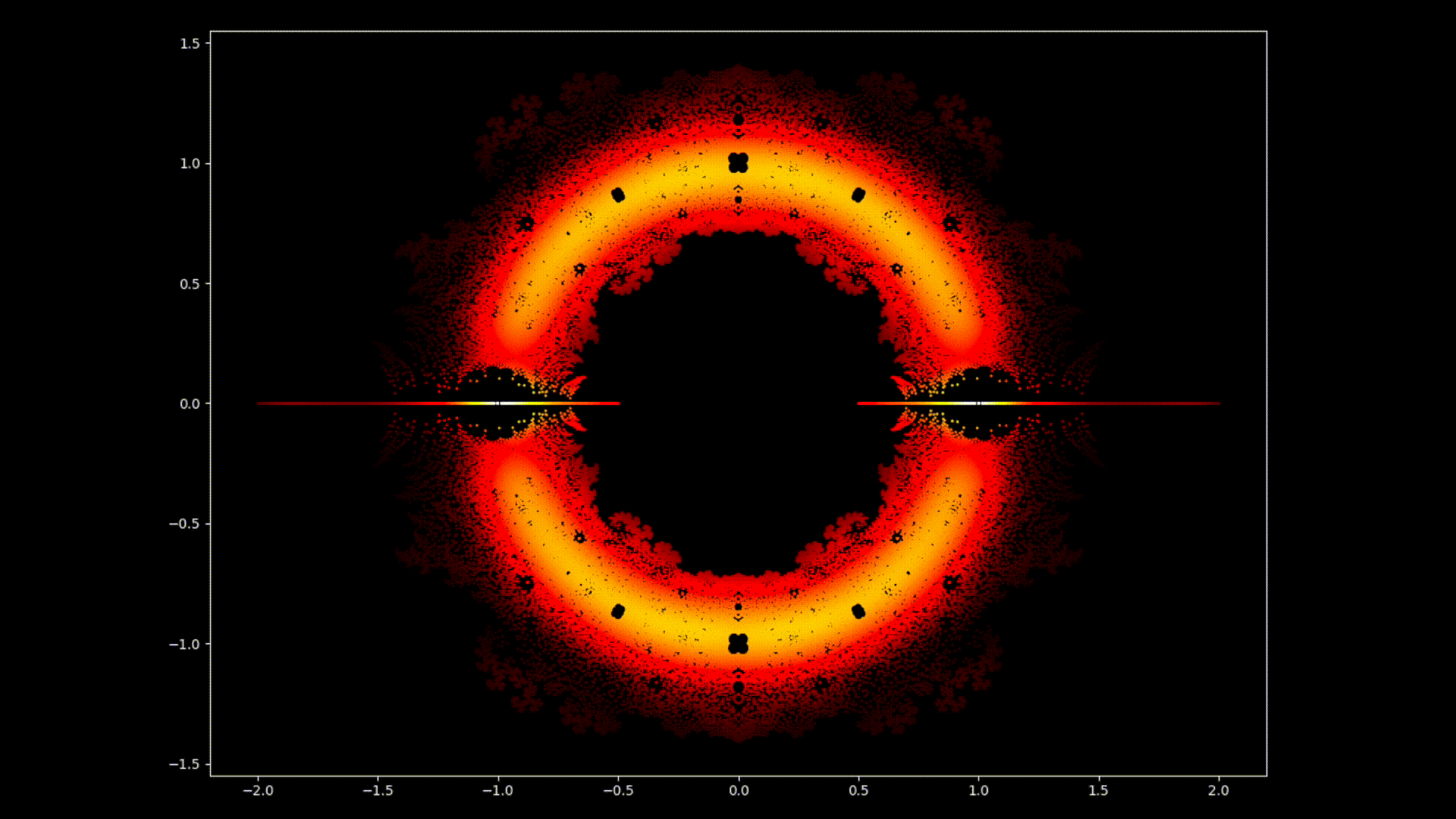
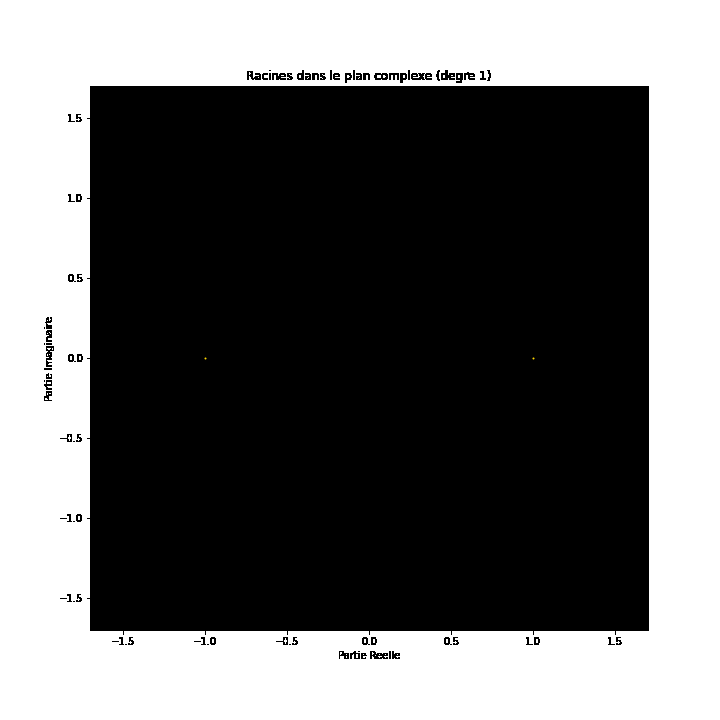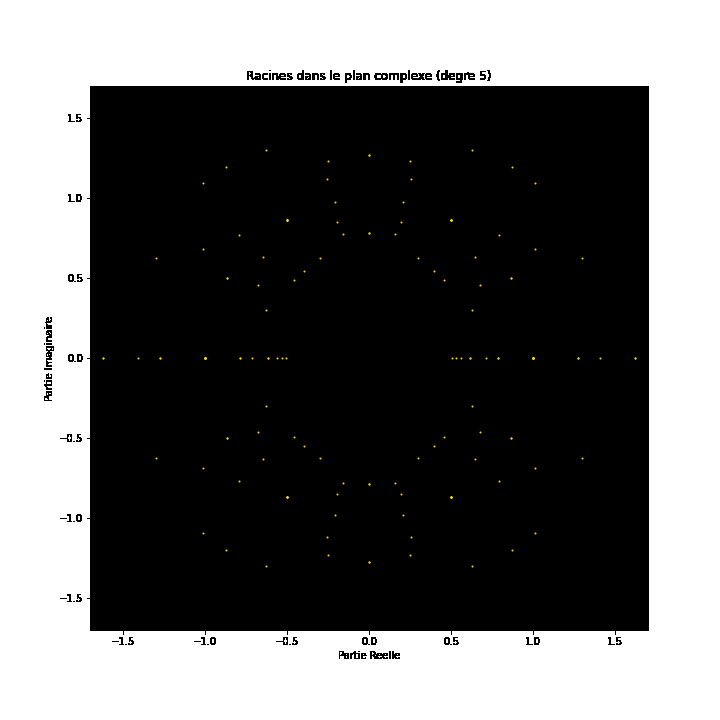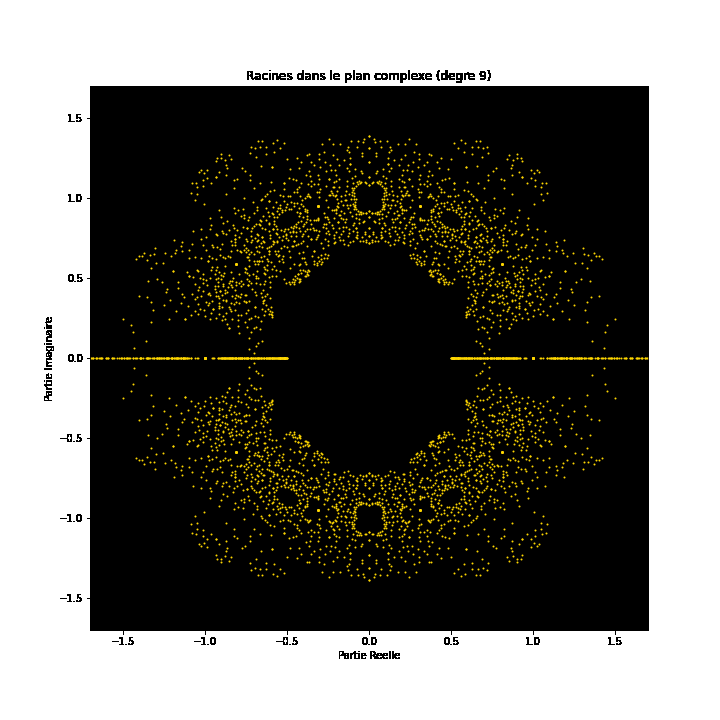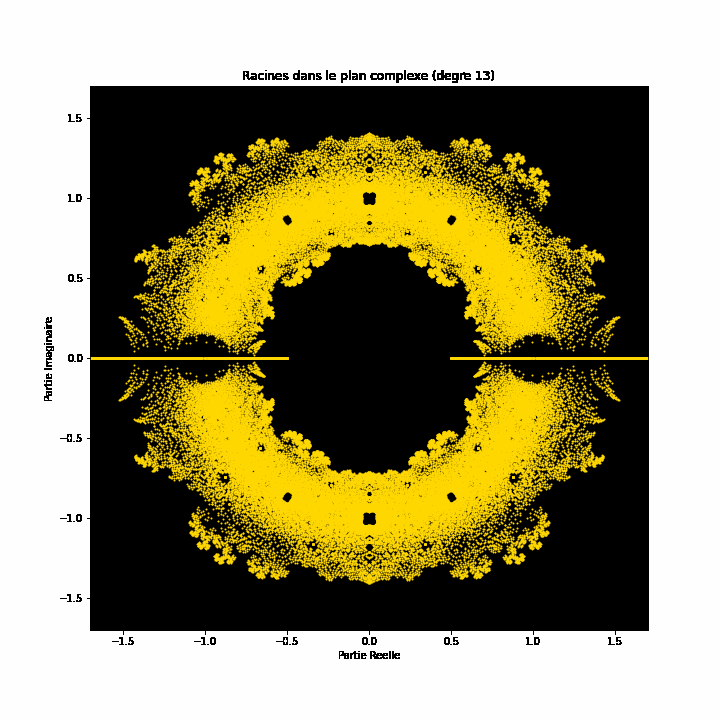
Op den éischte Bléck kënne Polynomgleichunge wéi abstrakt Konstruktioune schéngen, déi Kollektioune vun Zuelen a Variabelen op eng arbiträr Manéier arrangéiert. Allerdéngs läit ënner dëser Uewerfläch eng verstoppten Uerdnung an eng symmetresch Harmonie déi drop waarden entdeckt ze ginn. D'Léisunge vun enger Equatioun, bekannt als Wuerzele vum Polynom, halen eng déif Verbindung zum Konzept vun der Symmetrie. Dës Symmetrie kann och an de Biller vun dësem EML-Projet fonnt ginn, an deem mir d'Wuerzele vu Polynome mat Koeffizienten 1 an -1 beobachte kënnen, déi op engem komplexe Plang op eng symmetresch Manéier visualiséiert ginn, andeems e Punkt fir all Wuerzel gemoolt gëtt. Reell Wuerzelen erschéngen op der horizontaler Achs a komplex Wuerzelen op der vertikaler Achs. Mir kënnen déi eenzel Punkte fir all Wuerzel net gesinn, well et der ze vill sinn. Tatsächlech ginn et 805.306.368 Wuerzele fir e Polynom vum 24. Grad, déi all zesummen eng bizar Feierkugel bilden. Dës visuell Representatioune bidden Abléck an d'Verdeelung, d'Symmetrie an d'Behuele vun de polynomiale Wuerzelen, an hëllefen eis hir Eegenschaften a Relatiounen ze verstoen, awer si weisen och wéi schéi Mathematik ka sinn.

Krediter: Dës Biller goufen am Kader vum Experimental Mathematics Lab-Projet mam Titel ''Visualising roots of algebraic numbers'' erstallt, wou vill Studenten involvéiert waren, nämlech Claudia Marichal, Catia Alves Piro, Salma Belmir, Mikala Eisen, Melissa Genoud, Lynn Hellenbrand, Tom Kasel , Christophe Thelen, Gil Moes, Mirza Muharemovic, an et gouf vum Prof. Gabor Wiese, Dr. Guendalina Palmirotta an Dr. Thierry Meyrath betreit.

Weider Informatiounen: Kukt John Baez Websäit "The beauty of roots" an eis Experimental Mathematics Lab Websäit.

Aner Sproochen: